ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー１２（外接２円の中心と接点）
もし
　二つの円が
　外側で互いに接するならば、
　それらの中心を結ぶ線分は
　接点を通るであろう。

• 円は、定義１ー１５ による。
• 外側は、命題の補足３（定義１ー１４）による。
• 接するは、定義３ー３ による。
• 中心は、定義１ー１６ による。
• 線分は、定義の補足（命題１ー１） による。
• 接点は、定義３ー２の補足３ による。

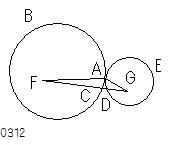
２円ＡＢＣ、ＡＤＥが
　外側で
　点Ａにおいて互いに接するとし、
　ＡＢＣの中心Ｆ、
　ＡＤＥの中心Ｇが
　とられたとせよ。 【・・・(a)】

• 命題３ー１（作図.円の中心） による。
• 　円ＡＢＣ
  に対して、
  　円ＡＤＥ[;;円ＡＤＥ;外側.円ＡＢＣ]、
  　接点Ａ(円ＡＤＥ,円ＡＢＣ)、
  　中心Ｆ.円ＡＢＣ、
  　中心Ｇ.円ＡＤＥ
  をとっている。

Ｆ、Ｇを結ぶ線分は

• 公準１ー１（作図.直線） による。

Ａにおける接点［接点Ａ］を
　通るであろう
　と主張する。

• 定義１ー１４の補足（交わる(図形)） により
  　線分ＦＧは
  　２円の周と交わる。
  その交点が
  　接点Ａである
  　ということである。

そうでないとすれば、

• 背理法の仮定を以下に述べている。

もし可能ならば

• 「もし可能ならば」は、
  コメント２(命題１−７）参照のこと。

ＦＣＤＧのようになるとし、

• 線分ＦＧが
  　定義１ー１４の補足（交わる(図形)）
  により
  　２円ＡＢＣ、ＡＤＥの周と交わる。
  その交点を
  　それぞれＣ、Ｄとして、
  　溯ってＣ、Ｄを用いている。
• 　交点Ｃ(線分ＦＧ,円ＡＢＣ);外.Ａ、
  　交点Ｄ(線分ＦＧ,円ＡＤＥ);外.Ａ
  をとったとしている。

ＡＦ、ＡＧが結ばれたとせよ。

• 公準１ー１（作図.直線） による。
• 　線分ＡＦ、ＡＧ
  をとっている。

そうすれば
点Ｆは
　円ＡＢＣの中心であるから、
ＦＡは
　ＦＣに等しい。 【・・・(1)】
また
点Ｇは
　円ＡＤＥの中心であるから、
ＧＡは
　ＧＤに等しい。

• (a) 定義１ー１５（円） による。
• 　ＦＡ＝ＦＣ、
  　ＧＡ＝ＧＤ
  となっている。

ところが
ＦＡが
　ＦＣに等しい
　ことも先に証明された。

• (1) による。
• 　ＦＡ＝ＦＣ
  となっている。

それゆえ
ＦＡ、ＡＧの和は
　ＦＣ、ＧＤの和に等しい。

• 公理１ー２（等しいものに等しいものを加える） による。
• 　ＦＡ＋ＡＧ＝ＦＣ＋ＧＤ
  となっている。

ゆえに
ＦＧ全体は
　ＦＡ、ＡＧの和より大きい。

• 公理１ー８（大きい）、 公理１ー８の補足２（等より大・小、大・小に等） による。
• 　ＦＧ＞ＦＡ＋ＡＧ
  となっている。

ところが、
　また小さくもある。

• 命題１ー２０（三角形の２辺の和と１辺） による。
• 　ＦＧ＜ＦＡ＋ＡＧ
  となっている。

これは不可能である。

• 背理法の仮定により矛盾が生じている。

したがって
Ｆ、Ｇを結ぶ線分は
　点Ａにおける接点を
　通らないことはないだろう。

• 背理法による。
• 　Ａ;上.ＦＧ
  となっている。

よってもし
　二つの円が
　外側で互いに接するならば、
それらの中心を結ぶ線分は
　接点を通るであろう。
　
これが証明すべきことであった。

• 命題３ー６の補足(接する２円の接点と中心は１直線上) で述べた内容の一部である。
• 命題3-12は、
  　円ＡＢＣ
  に対して、
  　円ＡＤＥ[;;円ＡＤＥ;外側.円ＡＢＣ]、
  　接点Ａ(円ＡＤＥ,円ＡＢＣ)、
  ならば、
  　Ａ;上.線分(中心Ｆ.円ＡＢＣ,中心Ｇ.円ＡＤＥ)
  のことである。
  
• 命題3-12は 推論用命題である。

  前提	作図	推論
  定義		1-14補 ,1-15
  公準	1-1
  公理		1-2 ,1-8 ,1-8補2
  命題	3-1	1-20
  その他		背理法,コ2(題1-7)

前 　　 次 　　 目次 　　頁頭