ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー４（弦の交点）
もし
　円において
　中心を通らない弦が
　互いに交わるならば、
　互いに２等分しない。

• 円は定義１ー１５による。
• 中心は定義１ー１６による。
• 弦は定義３ー４の補足による。
• 交わるは定義１ー１４の補足による。
• 等分は定義の補足２（公理１ー６）による。

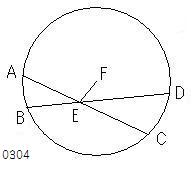
ＡＢＣＤを円とし、
　それにおいて
　中心を通らない２つの弦ＡＣ、ＢＤが
　Ｅにおいて
　互いに交わるとせよ。

• 　円ＡＢＣＤ
  をとり、
  　弦ＡＣ.円ＡＢＣＤ;(外)中心.円ＡＢＣＤ、
  　弦ＢＤ.円ＡＢＣＤ;(外)中心.円ＡＢＣＤ、
  　交点Ｅ(ＡＣ,ＢＤ)
  をとっている。

それらは
　互いに２等分しない
　と主張する。

• 「互いに２等分しない」とは、
  　「互いに２等分している
  　ということはない」
  　ということである。
  　一方だけを他方が２等分することは、
  　当然ありうる。

もし可能ならば

• 「もし可能ならば」は、
  コメント２(命題１−７）参照のこと。

互いに２等分し、
　ＡＥはＥＣに、
　ＢＥはＥＤに等しいとせよ。 【・・・(a)】

• 背理法の仮定である。
• 　ＡＥ＝ＥＣ、
  　ＢＥ＝ＥＤ
  としている。

円ＡＢＣＤの中心がとられ、
　それをＦとし、 【・・・(b)】

• 命題３−１（作図.円の中心）
  による。
• 　中心Ｅ.円ＡＢＣＤ
  となっている。

ＦＥが結ばれたとせよ。

• 公準１ー１（作図.直線）
  による。
• 　線分ＦＥ
  をとっている。

［このとき、
　角ＦＥＢ、ＦＥＤのいずれかの内部に、
　ＥＡかＥＣかのどちらかがふくまれる。
ここであらためて、
　含まれる方の円周上の点をＡ、
　　含まれない方をＣとし、
　含む方の円周上の点をＢ、
　　含まない方をＤとし、
　角ＦＥＢの中にＡがあるものとする。 【・・・(c)】］
　
そうすれば
　中心を通る線分ＦＥが
　中心を通らない弦ＡＣを２等分するから、
　それをまた直角に切る。

• (a) ,命題３−３（直径と弦）
  による。
• 　ＦＥ⊥ＡＣ
  となっている。

それゆえ
　角ＦＥＡは直角である。 【・・・(1)】

• 　前節による。
• 　∠ＦＥＡ＝∠Ｒ
  となっている。

また
　線分ＦＥが弦ＢＤを２等分するから、
　それをまた直角に切る。

• (a) ,命題３−３（直径と弦）
  による。
• 　ＦＥ⊥ＢＤ
  となっている。

ゆえに
　角ＦＥＢは直角である。

• 　前節による。
• 　∠ＦＥＢ＝∠Ｒ
  となっている。

しかも
　角ＦＥＡが直角なる
　ことも先に証明された。

• (1) による。
• 　∠ＦＥＡ＝∠Ｒ
  となっている。

したがって
　角ＦＥＡは角ＦＥＢに、
　すなわち
　小さいものが大きいものに等しい。

• 　公理１ー１（同じものに等しい）
  による。
  一方、
  (c) 公理１ー８（大きい）
  により、角ＦＥＢは角ＦＥＡより大きい。
• 　∠ＦＥＢ＝∠ＦＥＡ、
  かつ、
  　∠ＦＥＢ＞∠ＦＥＡ、
  となっている。

これは不可能である。

ゆえに
　ＡＣ、ＢＤは互いに２等分しない。

• 背理法による。
• 　Ｅ;¬(中点(ＡＣ)かつ中点(ＢＤ))
  となっている。

よってもし
　円において
　中心を通らない弦が互いに交わるならば、
　互いに２等分しない。
　
［これが証明すべきことであった。］

• 命題３−４は、
  　円ＡＢＣＤ
  に対して、
  　弦ＡＣ.円ＡＢＣＤ;(外)中心.円ＡＢＣＤ、
  　弦ＢＤ.円ＡＢＣＤ;(外)中心.円ＡＢＣＤ、
  をとれば、
  　交点Ｅ(ＡＣ,ＢＤ);¬(中点(ＡＣ)かつ中点(ＢＤ))
  のことである。
• 命題３−４は推論用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理		1-1,1-8
  命題	3-1	3-3
  その他		背理法,コ2(題1-7)

前 　　 次 　　 目次 　　頁頭