ユークリッド原論をどう読むか(5)
頁末
前
次
目次
ユークリッド原論
第2巻
命題2ー12(鈍角三角形の余弦定理)
「任意」
鈍角三角形において
鈍角の対辺の上の正方形
は
鈍角をはさむ2辺の上の正方形の和
より、
鈍角をはさむ辺の一つと、
この辺へと垂線が下され、
この鈍角への垂線によって
外部に切り取られた線分と
にかこまれた矩形の2倍だけ大きい。
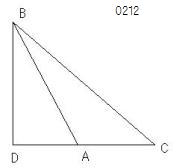
ABCを
鈍角BACをもつ鈍角三角形
とし、
点Bから
CAに垂線BDがひかれた
とせよ。
-
命題1ー12(作図・線分への垂線)
による。
-
△ABC;△(∠A>∠R)、
D;点(CAの延長上、BD⊥CA)
のことである。
BC上の正方形
は
BA、AC上の正方形の和より
CA、ADにかこまれた矩形の2倍だけ大きい
と主張する。
線分CD
は
点Aにおいて任意に分けられた
-
「任意に」
という表現は
直後の推論に用いる命題2ー4の表現に
合わせた
ためであろう。
証明の途上に現れる「任意」
は、
このような場合が多い。
「任意」の意味を理解しない
後世の解説者のコメントが
紛れ込んだ
と考えられる。
(以下、コメント(命題2ー12)(任意)という。)
-
命題の設定による。
-
A;点(CD)
となっている。
から、
DC上の正方形
は
CA、AD上の正方形と
CA、ADにかこまれた矩形の2倍と
の和に等しい。
-
前節、
命題2ー4(2分線分上の正方形)
による。
-
sq(_DC)=sq(_CA)+sq(_AD)+2×rec(CA、AD)
となっている。
双方に
DB上の正方形が加えられた
とせよ。
そうすれば
CD、DB上の正方形の和
は
CA、AD、DB上の正方形と
矩形CA、ADの2倍と
の和に等しい。
-
前節、前々節、
公理1ー2(等しいものに等しいものを加える)
による。
-
sq(_DC)+sq(_DB)
=sq(_CA)+sq(_AD)+sq(_DB)
+2×rec(CA、AD)
となっている。
ところが
Dにおける角
は
直角である
から、
CB上の正方形
は
CD、DB上の正方形
の和に等しい。
-
前節、
命題1ー47(三平方の定理)
による。
-
sq(_DC)+sq(_DB)=sq(_CB)
となっている。
[ゆえに
CB上の正方形
は
CA、AD、DB上の正方形と
矩形CA、ADの2倍と
の和に等しい。]
-
前節、前々々節、
公理1ー1(同じものに等しい)
による。
-
sq(_CB)
=sq(_CA)+sq(_AD)+sq(_DB)
+2×rec(CA、AD)
となっている。
そして
AB上の正方形
は
AD、DB上の正方形
の和に等しい。
-
命題の設定
、
命題1ー47(三平方の定理)
による。
-
sq(_AB)=sq(_AD)+sq(_DB)
となっている。
ゆえに
CB上の正方形
は
CA、AB上の正方形と
CA、ADによってかこまれた矩形の2倍と
の和に等しい。
-
前節、前々節、
公理1ー2(等しいものに等しいものを加える)、
公理1ー1(同じものに等しい)
による。
-
sq(_CB)=sq(_CA)+sq(_AB)+2×rec(CA、AD)
となっている。
したがって
CB上の正方形
は
CA、AB上の正方形の和より
CA、ADにかこまれた矩形の2倍
だけ大きい。
よって
鈍角三角形において
鈍角の対辺の上の正方形
は
鈍角をはさむ2辺の上の正方形
の和より、
鈍角をはさむ辺の一つと、
この辺へと垂線が下され、
この鈍角への垂線によって
外部に切り取られた線分と
にかこまれた矩形の2倍
だけ大きい。
これが証明すべきことであった。
- いわゆる
余弦定理の鈍角三角形の場合である。
-
△ABC;△(∠A>∠R)
に対して、
D;点(CAの延長上、BD⊥CA)
をとれば、
sq(_CB)
=sq(_CA)+sq(_AB)
+2×rec(CA、AD)
のことである。
- 命題2-12は推論用命題である。
前
次
目次
頁頭
