ユークリッド原論をどう読むか（３）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー２５（三角形の角と底辺２）
もし二つの三角形において
　２辺が２辺にそれぞれ等しく、
　底辺が底辺より大きいならば、
　等しい線分にはさまれる角も
　一方が他方より大きいであろう。

• 三角形は、定義１ー１９の補足２による。
• 辺は、定義１ー１９の補足による。
• 等しいは、公理１ー７による。
• 底辺は、定義１ー２０の補足２による。
• 大きいは、公理１ー８による。
• 線分は、定義１ー４の補足による。
• 角は、定義１ー８による。

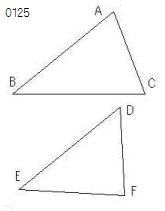
ＡＢＣ、ＤＥＦを
　２辺ＡＢ、ＡＣが２辺ＤＥ、ＤＦにそれぞれ等しい、
　すなわちＡＢはＤＥに、ＡＣはＤＦに等しい
　三角形とせよ。
そして
　底辺ＢＣが底辺ＥＦより大きいとせよ。

• 　△ＡＢＣ
  をとり、
  　点Ｃ'[ＢＣ;;ＢＣ'＋ＣＡ＞ＡＢ,ＡＢ＋ＢＣ'＞ＣＢ]
  をとり、
  　命題１ー２２（作図・３線分から三角形）
  により、
  　線分ＤＥ、ＢＣ'、ＤＦ
  から
  　△ＤＥＦ
  をとる。
  
• 　(ＡＢ,ＡＣ)＝(ＤＥ,ＥＦ)、
  　ＢＣ＞ＥＦ
  となっている。

角ＢＡＣも角ＥＤＦより大きいと主張する。

もし大きくないならば、
　それに等しいか小さいかである。

• 　第一段階の背理法の仮定である。
• 　公理１ー７の補足（等しい）
  による。

ところで
　角ＢＡＣは角ＥＤＦに等しくない。
なぜなら［もし
　角ＢＡＣが角ＥＤＦに等しいとすると

• 　「なぜならもし」については、
  　コメント（命題１ー４）を参照のこと。
• 　第二段階の背理法の仮定である。
• 　∠ＢＡＣ＝∠ＥＤＦ
  としている。

］
底辺ＢＣも底辺ＥＦに等しくなるであろう。

• 　命題１ー４（２辺挟角相等）
  による。
• 　ＢＣ＝ＥＦ
  となっている。

ところがそうではない。

• 命題の設定 による。

それゆえ
　角ＢＡＣは角ＥＤＦに等しくはない。
　　　　　　【・・・(1)】

• 　第二段階の背理法による。
• 　∠ＢＡＣ≠∠ＥＤＦ
  となっている。

また
　角ＢＡＣは角ＥＤＦより小さくもない。
なぜなら
　［もし角ＢＡＣが角ＥＤＦより小さいとすると

• 「なぜならもし」については、
  　コメント（命題１ー４）を参照のこと。
• 　再度、第二段階の背理法の仮定である。

］

底辺ＢＣも底辺ＥＦより小さくなるであろう。

• 　命題１ー２４（三角形の角と底辺１）
  による。

ところがそうではない。

• 命題の設定 による。

それゆえ
　角ＢＡＣは角ＥＤＦより小さくない。

• 　第二段階の背理法による。

また、
　等しくないことも先に証明された。

• 　(1) による。

ゆえに
　角ＢＡＣは>角ＥＤＦより大きい。

• 　第一段階の背理法による。

よってもし
　二つの三角形において
　2辺が2辺にそれぞれ等しく、
　底辺が底辺より大きいならば、
　等しい線分にはさまれる角も
　一方が他方より大きいであろう。
　
これが証明すべきことであった。

• 　命題1-25は、
  　△ＡＢＣ、△ＤＥＦ
  について、
  　(ＡＢ,ＡＣ)＝(ＤＥ,ＤＦ)、
  　ＢＣ＞ＥＦ
  ならば、
  　∠ＢＡＣ＞∠角ＥＤＦ
  のことである。
• 　命題1-25は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理		1-7補
  命題		1-4、1-24
  その他		二段階までの背理法、コ(題1-4)ft

前 　　 次 　　 目次 　　頁頭