ユークリッド原論をどう読むか（１６）
頁末 　　 前 　　 次 　 目次

ユークリッド原論

第１０巻
　
命題１０ー１１５（有理線分と、中項線分との比例中項は無理線分、さらにその比例中項は新たな無理線分）
　　中項線分から
　無数の無理線分が
　　　生じ、
　それらのどれも
　　前のもののどれとも
　　　同じでない。

• 中項線分は、
  定義の補足（命題１０ー２１）による。
• 無理線分は、
  定義１０ー４の補足による。

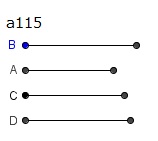
　　Ａを中項線分
とせよ。

• 　命題１０ー２２の補足 (作図.中項線分)
  による。
• 　Ａ；中項線分
  となっている。

　　Ａから
　無数の無理線分が
　　　生じ、
　それらのどれも
　　前のもののどれとも
　　　同じでない
と主張する。

　有理線分Ｂが
　　　定められ、
　　Ｃ上の正方形を
　　矩形Ａ、Ｂ
　　　に等しくせよ。

• 　命題の補足２（定義１０ー３）(作図.任意の有理線分)、
  　命題６ー１７の補足 (作図.線分上に矩形と等しい正方形)
  による。
• 　Ｂ；有理線分、
  　辺Ｃ.正方(_；＝矩形(Ａ、Ｂ))
  となっている。

そうすれば
　Ｃは
　　無理線分
　　　である。
なぜなら
　　無理線分と有理線分とによって
　　　かこまれる
　矩形は
　　無理面積
　　　である
から。

• 背理法の仮定として、
  もし、
  　　有理面積
  　　　であるとすると、
  　命題１０ー２０（有理線分上の有理面積の矩形幅は底辺と長さで通約）
  により、
  　Ａは、
  　　有理線分
  　　　となり、
  　矛盾が生じる
  から。
  
• 　なぜならは、
  　コメント（命題１ー４）を
  　　　参照のこと。
• 　Ｃ；無理線分
  となっている。

そして
　　前のもののどれとも
　　　同じでない。
なぜなら
　　前のもののどれの上の正方形
　　　に等しい
　矩形も
　　有理線分上に
　　　つくられる
ならば、
　　中項線分を幅
　　　としない
から。
　　　　[......(１)]

• 　命題１０ー２２（中項線分上正方形に等矩形で底辺有理線分なら幅は有理で非通約）
  　辺ＸＡ.矩形(Ｂ、ＸＡ；＝正方(_Ａ)）
  　　；有理線分、¬∩Ｂ、
  　命題１０ー２０（有理線分上の有理面積の矩形幅は底辺と長さで通約）
  により、
  　辺ＸＢ.矩形(Ｂ、ＸＢ；＝正方(_Ｂ)）
  　　＝Ｂ；有理線分
  となり、
  　辺ＸＣ.矩形(Ｂ、ＸＣ；＝正方(_Ｃ)＝矩形(Ａ、Ｂ)）
  　　＝Ａ；中項線分、
  と異なるから。
• 　Ｃ≠Ａ、≠Ｂ
  となっている。

また
　　Ｄ上の正方形を
　　矩形Ｂ、Ｃ
　　　に等しくせよ。
そうすれば
　Ｄ上の正方形は
　　無理面積である。

• 背理法の仮定として、
  もし、
  　有理面積であるとすると、
  　命題１０ー２０（有理線分上の有理面積の矩形幅は底辺と長さで通約）
  により、
  　Ｃは有理線分
  となり、
  　矛盾が生じる
  から
  
• 　正方(_Ｄ)；無理面積
  となっている。

ゆえに
　Ｄは
　　無理線分
　　　である。

• 　前節
  　定義１０ー４（面積の有理、無理、無理線分）
  による。
• 　Ｄ；無理線分
  となっている。

そして
　　前のもののどれとも
　　　同じでない。
なぜなら
　　前のもののどれの上の正方形
　　　に等しい
　矩形も
　　有理線分上に
　　　つくられる
ならば、
　　Ｃを幅
　　　としない
から。

• 　命題１０ー２２（中項線分上正方形に等矩形で底辺有理線分なら幅は有理で非通約）
  により、
  　辺ＸＡ.矩形(Ｂ、ＸＡ；＝正方(_Ａ)）
  　　；有理線分、¬∩Ｂ、¬Ｃ、
  　命題１０ー２０（有理線分上の有理面積の矩形幅は底辺と長さで通約）
  により、
  　辺ＸＢ.矩形(Ｂ、ＸＢ；＝正方(_Ｂ)）
  　　＝Ｂ；有理線分、¬Ｃ、
  　辺ＸＣ.矩形(Ｂ、ＸＣ；＝正方(_Ｃ)＝矩形(Ａ、Ｂ)）
  　　＝Ａ；中項線分、¬Ｃ
  となり、
  　辺ＸＤ.矩形(Ｂ、ＸＤ；＝正方(_Ｄ)＝矩形(Ｂ、Ｃ)）
  　　＝Ｃ
  と異なるから。
• 　Ｄ；¬（Ａ、Ｂ、Ｃ）
  となっている。

同様にして
もし
　このような操作が
　　　限りなく進め
ば、
　　中項線分から
　無数の無理線分が
　　　生じ、
　それらのどれも
　　前のもののどれとも
　　　同じでない
ことは明らかである。

• 　有理線分Ｂと無理線分Ｃｎについて、
  　辺Ｃn+1.正方(_；＝矩形(Ｂ、Ｃn))
  とすると、
  　Ｃn+1；無理線分
  となる。
  なぜなら、
  　Ｃn+1；有理線分
  
  となれば、　
  　命題１０ー２０（有理線分上の有理面積の矩形幅は底辺と長さで通約）
  により、
  　辺Ｘn+1.矩形(Ｂ、Ｘn+1；＝正方(_Ｃn+1)＝矩形(Ｂ、Ｃn)）
  　　＝Ｃn、；有理線分
  となり、
  　Ｃn；無理線分
  と矛盾するから。
  また、
  　Ｃn+1はＢとＣnの間
  となる。
  なぜなら、
  　命題６ー１７（比例３線分と外項矩形、中項正方形） により、 　Ｂ：Ｃn+1＝Ｃn+1：Ｃn
  となり、
  　命題６ー１３の補足(比例中項は２項の間)
  により
  　Ｃn+1はＢとＣnの間
  となるから。
  よって、
  　Ｃn+1は、
  　　Ｃ1、Ｃ2、･･･、Ｃn
  　　　と異なる。
  
• 　Ｅ≠Ａ、Ｂ、Ｃ、Ｄ
  となっている。

これが証明すベきことであった。

• 命題１０ー１１５は、
  　命題の補足２（定義１０ー３）(作図.任意の有理線分)、
  により、
  　有理線分Ｂ
  をとり、
  　命題１０ー２２の補足(作図.中項線分)
  により、
  　Ａを中項線分
  をとり、
  　命題６ー１７の補足(作図.線分上に矩形と等しい正方形)
  により、
  　辺Ｃ.正方(_；＝矩形(Ｂ、Ａ))
  をとれば、
  　Ｃ；無理線分、ＢとＡの間
  となり、
  その後、順に、
  　辺Ｃn+1.正方(_；＝矩形(Ｂ、Ｃn))
  とすれば、
  　Ｃn+1；無理線分、≠（Ｃ1、Ｃ2、･･･、Ｃn）
  のことである。
• 命題１０ー１１５は推論用命題である。

  前提	作図・構成	推論
  定義		10-4
  公準
  公理
  命題	6-17補,10-22補,補2(義10-3)	6-13補,6-17,10-20,10-22
  その他	コ(題1-4)

前 　　 次 　　 目次 　　頁頭