ユークリッド原論をどう読むか（１２）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第８巻
　
命題８ー１５（立方数の整除、辺の整除）
もし
　立方数が立方数を割り切る
ならば、
　辺も辺を割り切る
であろう。

そしてもし
　辺が辺を割り切る
ならば、
　立方数も立方数を割り切る
であろう。

• 立平方数は、
  定義７ー２０による。
• 割り切るは、
  定義５ー１の補足２による。
• 辺は、
  定義７ー１８の補足による。

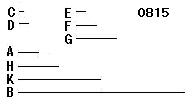
　立方数Ａが
　立方数Ｂを割り切る
とし、
　ＣをＡの、ＤをＢの辺
とせよ。

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
  
• Ｃ×Ｃ×Ｃ＝Ａ、Ｄ×Ｄ×Ｄ＝Ｂ、
  　Ａ｜Ｂとなっている。
  

　ＣはＤを割り切る
と主張する。

　Ｃが２乗してＥをつくり、
　Ｄが２乗してＧをつくり、
さらに
　ＣがＤにかけてＦをつくり、
　Ｃ、ＤがＦにかけて
　それぞれＨ、Ｋをつくる
とせよ。

• 　Ｃ×Ｃ＝Ｅ、Ｄ×Ｄ＝Ｇ、
  　Ｃ×Ｄ＝Ｆ、
  　Ｃ×Ｆ＝Ｃ×Ｃ×Ｄ＝Ｈ、
  　Ｄ×Ｆ＝Ｄ×Ｃ×Ｄ＝Ｋ
  となっている。
  　命題７ー１６　（積の可換性）
  により、
  　Ｄ×Ｆ＝Ｆ×Ｄ＝Ｃ×Ｄ×Ｄ＝Ｋ
  　となっている。
  

そうすれば
　Ｅ、Ｆ、ＧとＡ、Ｈ、Ｋ、Ｂは
　Ｃ対Ｄの比をなして
　順次に比例する
ことは明らかである。
　　　　　　[......(１)]

• 　命題８ー１１の補足２
  　（平方数の比例中項）、
  　命題８ー１２の補足
  　（立方数の比例中項）
  による。
  

そして
　Ａ、Ｈ、Ｋ、Ｂは
　順次に比例し、
　ＡはＢを割り切る

• 　前節、
  　命題の設定による。

から、
　Ｈをも割り切る。

• 　命題８ー７
  　（順次比例で初項が末項の約(倍)数）
  による。

そして
　ＡがＨに対するように、
　ＣがＤに対する。

• 　（１）による。

したがって
　ＣもＤを割り切る。

• 　前節、前々節、
  　定義７−２１（比例）
  による。
  
• 　前半が証明された。

次に
　ＣがＤを割り切る
とせよ。

• 　Ｃ｜Ｄとなっている。

　ＡもＢを割り切る
であろうと主張する。

　同じ作図がなされた
とき、

• 　Ｃ×Ｃ＝Ｅ、Ｄ×Ｄ＝Ｇ、
  　Ｃ×Ｄ＝Ｆ、
  　Ｃ×Ｆ＝Ｃ×Ｃ×Ｄ＝Ｈ、
  　Ｄ×Ｆ＝Ｆ×Ｄ＝Ｃ×Ｄ×Ｄ＝Ｋ
  　を構成している
  ことを述べている。
  

　同様にして
　Ａ、Ｈ、Ｋ、Ｂが
　Ｃ対Ｄの比をなして
　順次に比例する
ことを証明しうる。
　　　　　　[......(２)]

• 　命題８ー１２の補足
  　（立方数の比例中項）
  による。
  

そして
　ＣがＤを割り切り、
　ＣがＤに対するように、
　ＡがＨに対する

• 　前節、
  命題の設定による。

から、
　ＡもＨを割り切る。

• 　定義７−２１（比例）
  による。 　

［ そして
　Ａ、Ｈ、Ｋ、Ｂは順次に比例する。

• 　（２）による。

］
したがって
　ＡもＢを割り切る。

• 　前節、前々節により
  　前項は後項を割り切る
  ので、
  　公理の補足２（命題７ー４）
  　（約数(倍数)での代入の原理）
  による。
  
• 　後半が証明された。

これが証明すべきことであった。

• 　Ｃ^3｜Ｄ^3　なら　Ｃ｜Ｄ
  のことである。
• 命題８ー１５は推論用命題である。

  前提	作図	推論
  定義		7-21
  公準
  公理		補2(題7-4)
  命題		8-7,8-11補2,8-12補
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭