ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー３７（割り切れるなら同名の等分数が存在）
同名の等分(数)
(同名の等分に同じ等分)
もし
　ある数が
　ある数に割り切られる
ならば、
　割り切られる数は
　割り切る数と同名の《約数》［等分数］をもつ
であろう。

• 数は、 定義７ー２による。
• 割り切るは、 定義５ー１の補足２による。
• 定義の補足２（公理１ー６）（ｎ等分・ｎ分の１）
  により、
  　数Ａをある個数に等分するとき、
  特に個数を明示して、
  　Ｃ個に等分することを
  　Ｃと同名の等分
  といい、
  　Ａを、Ｃと同名の等分にした結果を、
  特に、数として強調する場合、
  　Ａの、Ｃと同名の等分数という。
  (以下、定義の補足（命題７ー３７） (同名の等分(数))という。)
  すなわち、
  　Ｃと同名の等分とは、
  　今日的に表現すれば、
  　１／Ｃ
  のことである。
  　(Ｂ、単位Ｄ)が、
  　(Ａ、Ｃ)を同じ個数に等分して得られるとき、
  　定義の補足（命題７ー５）（同じ等分）
  により、
  　ＢがＡのいかなる等分であっても、
  　単位ＤがＣの同じ等分であり、
  　等分(Ｂ,Ａ)＝等分(単位Ｄ,Ｃ)
  と表現し、
  　等分(単位Ｄ,Ｃ)は、
  　定義の補足（命題７ー３７）(同名の等分(数))
  により、
  　数Ｃの、Ｃと同名の等分であり、
  　等分(単位Ｄ,Ｃ);＝同名等分(Ｃ)
  と表現すると、
  　等分(Ｂ,Ａ)＝同名等分(Ｃ)
  となる。
  　単位Ｄは、
  　Ｄ;＝同名等分(Ｃ).Ｃ
  と表現すると、
  　ＢはＡのＣと同名の等分
  すなわち、
  　Ｂ＝同名等分(Ｃ).Ａ
  となっている。　
  よって、
  　等分(Ｂ,Ａ)＝等分(単位Ｄ,Ｃ)、
  ならば、
  　等分(Ｂ,Ａ)＝同名等分(Ｃ)
  　Ｂ＝同名等分(Ｃ).Ａ
  となっている。
  (以下、命題７ー３７の補足２(同名の等分に同じ等分)という。)
  割り切られる数に対して、
  同名の等分が、
  原論の現段階での数に近い存在として
  扱われているというのが、
  本命題の裏にある趣旨である。
  本命題のなかに、
  　単位Ｄは数Ｂの、
  　Ｂと同名の《約数》［等分］である。
  という表現がある。
  また、
  Euclid's Elements
  （Clark University Professor D.E.Joyceの
  http://aleph0.clarku.edu/~djoyce/java/elements/elements.html）
  　においては、
  This proposition says
  that
  if B divides A,
  then
  A has a one-Bth part(namely,A/B).
  と、コメントしている。
  なお、約数は、
  英文では a part である。
  また、a part は
  等分した１つ分という意味もある。
  この２つの意味を
  英文では（恐らくギリシャ文でも）
  併せて用いている。
  本解説では、
  前者を約数、
  後者を等分
  と区別している。
  

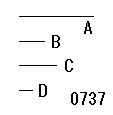
　数Ａが
　何らかの数Ｂに割り切られる
とせよ。

• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１） を参照のこと。
• 　数Ａ
  に対し、
  　数Ｂ[;;｜Ａ]
  をとっている。

　Ａは
　Ｂと同名の《約数》［等分数］をもつ
と主張する。

　ＢがＡを割った商と等しい
　個数の単位が
　Ｃのなかにある
とせよ。
　　　　　　[......(ａ)]

• 　数Ｃ(;;個数(Ｃ,単位)＝商(Ａ,Ｂ))
  をとっている。

　ＢがＡを割った商は
　Ｃのなかにある単位の個数であり、
　単位Ｄが数Ｃを割った商は
　Ｃのなかにある単位の個数である

• 定義７ー８の補足（商）
  による。
• 　商(Ｃ,単位Ｄ)＝個数(Ｃ,単位)
  となっている。

から、
　単位Ｄが数Ｃを、
　ＢがＡを
　割った商は等しい。

• （ａ）、前節による。
• 　商(Ｃ,単位Ｄ)＝個数(Ｃ,単位)、
  　商(Ｃ,単位Ｄ)＝商(Ａ,Ｂ)
  となっている。

それゆえ
　いれかえて
　単位Ｄが数Ｂを、
　ＣがＡを
　割った商は等しい。

• 命題７ー１５（割る数と商のいれかえ）
  による。
• 　商(Ｂ,単位Ｄ)＝商(Ａ,Ｃ)
  となっている。

ゆえに
　単位Ｄが数Ｂの
　いかなる《約数》[等分]で
あろうと、
　ＣもＡの
　同じ《約数》[等分]である。
　　　　　　[......(１)]

• 定義７ー８の補足（商）、
  定義の補足（命題７ー５）（同じ等分）
  による。
• 　等分(単位Ｄ,Ｂ)＝等分(Ｃ,Ａ)＝１／Ｂ、
  となっている。

ところが
　単位Ｄは数Ｂの、
　Ｂと同名の《約数》［等分］である。

• 定義の補足（命題７ー３７）(等分・同名の等分(数))
  による。
• 　等分(単位Ｄ,Ｂ)＝同名等分(Ｂ)、
  　単位Ｄ;同名等分(Ｂ).Ｂ＝単位
  となっている。

したがって
　ＣはＡの、
　Ｂと同名の《約数》［等分］である。

• （１）、前節、
  命題７ー３７の補足２(同名の等分に同じ等分)
  による。
• 　Ｃ;同名等分(Ｂ).Ａ
  となっている。

よって
　Ａは
　Ｂと同名の《約数》［等分数］Ｃをもつ。

• 　定義の補足（命題７ー３７） (同名の等分(数))
  による。

　これが証明すべきことであった。

• 等分・同名の等分という表現で
  ｎ分の１という単位分数の概念が
  発生し始めている。
  注目すべき命題である。
  
• 命題７ー３７は、
  　数Ａ、Ｂ[;;｜Ａ]
  に対して、
  　数Ｃ(;;個数(Ｃ,単位Ｄ)＝商(Ａ,Ｂ))
  をとれば、
  　Ｃ;同名等分(Ｂ).Ａ
  のことである。
  
• 命題７ー３７の補足２(同名の等分に同じ等分)

  前提	作図	推論
  定義		補(題7-5),補(題7-37)
  公準
  公理
  命題
  その他

• 命題７ー３７は推論用命題である。

  前提	作図	推論
  定義		補(題7-5),7-8補,補(題7-37)
  公準
  公理
  命題		7-15,7-37補2
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭