ユークリッド原論をどう読むか(11)
頁末
前
次
目次
ユークリッド原論
第7巻
命題7ー5(和も同じ等分)
同じ等分、
(構成.同じ等分となる第4数)、
(同じ等分に同じ)
もし
ある数がある数の《約数》[等分]であり、
別のある数が別のある数の
同じ《約数》[等分]であるならば、
1つが1つのいかなる《約数》[等分]であろうと、
和も同じ《約数》[等分]であろう。
- 数は、
定義7ー2
による。
- 等分は、
定義7ー3
による。
-
同じ等分
とは、
それぞれ
割り切る
に当たっての
個数が同じということである。
したがって、
同じ等分ならば
数は、それが割り切る数に対して
同じ比をもつ。
定義の補足(命題5ー1)
にいう
同じ倍数に対応する。
(以下、定義の補足(命題7ー5)(同じ等分)という。)
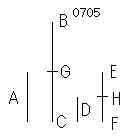
数AがBCの《約数》[等分]であるとし、
AがBCのいかなる《約数》[等分]であろうと、
別の数Dが別の数EFの
同じ《約数》[等分]であるとせよ。
-
「数(について)・・・とせよ」は、
コメント4(命題7ー1)
参照のこと。
図は、4、8、2、4による。
-
数BC、数Dと
BCの等分A
について、
数EFを、
DがEFの同じ等分となる
ように
取ることができる。
(以下、命題7ー5の補足2
(構成.同じ等分となる第4数)という。)
すなわち、
定義7ー3(約数・等分数)
により、
個数p(BC,A)
が定まり、
定義7ー16(かける)
により、
Dを
個数p(BC,A)の回数だけ加えて
EFとする
と、
定義の補足(命題7ー5)(同じ等分)
による。
-
数A、B、C、D、E、F
について、
BがAの等分であるように、
DがCの同じ等分であり、
また、
BがAの等分であるように、
FがEの同じ等分である
ならば、
DがCの等分であるように、
FがEの同じ等分である。
(以下、命題7ー5の補足3(同じ等分に同じ)という。)
というのは、
定義の補足(命題7ー5)(同じ等分)
により、
個数(A,B)=個数(C,D)、
個数(A,B)=個数(E,F)
となるので、
公理1ー1(同じものに等しい)
により、
個数(C,D)=個数(E,F)
となり、
定義の補足(命題7ー5)(同じ等分)
による。
-
数BC、数D、
数A;等分(A,BC)、
に対して、
数EF(;;等分(A,BC)=等分(D,EF))
をとっている。
A、Dの和もBC、EFの和の、
AがBCの《約数》[等分]であるのと
同じ《約数》[等分]である
と主張する。
AがBCのいかなる《約数》[等分]であろうと、
DもEFの同じ《約数》[等分]であるから、
- 命題の設定
による。
-
等分(A,BC)=等分(D,EF)
となっている。
BCのなかにある
Aに等しい数と同じ個数の、
Dに等しい数が
EFのなかにもある。
【・・・(1)】
BCが
Aに等しい数BG[=G1G'1、…、GiG'i、GnG'n=]GCに、
EFが
Dに等しい数EH[=H1H'1、…、HiH'i、HnH'n=]HFに
分けられたとせよ。
【・・・(a)】
-
推論の設定である。
-
2等分した場合で論証している
準一般的な証明である。
コメント2(命題5ー1)参照のこと。
-
BC=Σ(GiG'i;=A)、
EF=Σ(HiH'i;=D)
となっている。
そうすれば
BG、GCの個数は
EH、HFの個数に等しいであろう。
-
(1)による。
-
推論の設定として、
2等分の場合にしているが
可能な限り
一般的となるよう
推論が進められている。
-
個数(GiG'i)=個数(HiH'i)=n
となっている。
そして
BGはAに、
EHはDに等しいから、
-
(a)による。
-
BG=A、
EH=D
となっている。
BG、EHの和も
A、Dの和に等しい。
-
公理1ー2(等しいものに等しいものを加える)
による。
-
BG+EH=A+D
となっている。
同じ理由で
GC、HFの和も、
A、Dの和に等しい。
それゆえ
BCのなかにある
Aに等しい数と同じ個数の、
A、Dの和に等しい数が
BC、EFの和のなかにもある。
ゆえに
BCがAの何倍であろうと、
BC、EFの和も
A、Dの和の同じ倍数である。
したがって
AがBCのいかなる《約数》[等分]であろうと、
A、Dの和もBC、EFの和の同じ《約数》[等分]である。
-
等分(A,BC)=等分(A+D,BC+EF)
となっている。
これが証明すべきことであった。
- 命題7ー5は、
等分(A,BC)=等分(D,EF)
ならば、
等分(A,BC)=等分(A+D,BC+EF)
のことである。
-
命題7ー5の補足2 (構成.同じ等分となる第4数)
-
命題7ー5の補足3(同じ等分に同じ)
- 命題7ー5は推論用命題である。
前
次
目次
頁頭
