ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー１２（比例する前項・後項の総和）
もし
　任意個の数が比例する
ならば
　前項の１つが後項の１つに対するように、
　前項の総和が後項の総和に対するであろう。

• 数は、 定義７ー２による
• 比例は、 定義７ー２１による
• 前項は、 定義５ー１１の補足による
• 後項は、 定義５ー１１の補足２による
• 対する・ようには 定義の補足３（命題５ー１１） による。

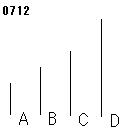
　Ａ、Ｂ、［Ｂi、Ｃi、］Ｃ、Ｄを比例する任意個の数
とし、

　ＡがＢに対するように、
［ＢiがＣiに対し、］
　ＣがＤに対する
とせよ。

• 準一般的な証明である。
  コメント２（命題５ー１） 参照のこと。
  準一般的な証明の一般化の方法は、
  　コメント５（命題５ー１）
  　参照のこと。
• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１） 参照のこと。
• 命題７ー１１の補足(構成.比例する数の作図)
  による。
  図は、Ａ＝２、Ｂ＝３、Ｃ＝４、Ｄ＝６による。
• 　Ａ：Ｂ＝Ｂi：Ｃi＝Ｃ：Ｄ＝ｎ：ｍ
  をとっている。

　ＡがＢに対するように、
　Ａ、［Ｂi、］Ｃの和がＢ、［Ｃi、］Ｄの和に対する
と主張する。

　ＡがＢに対するように、
［Ｂi、Ｃiに対し、］
　ＣがＤに対する

• 命題の設定 による。
• 　Ａ：Ｂ＝Ｂi：Ｃi＝Ｃ：Ｄ＝ｎ：ｍ
  となっている。

から、
　ＡがＢのいかなる《約数》[等分]または《約数》[等分]和であろう
と、
［ＢiもＣiの同じ《約数》[等分]または《約数》[等分]和であり、］
　ＣもＤの同じ《約数》[等分]または《約数》[等分]和である。

• 定義７ー２１（比例）
  による。
• 　等分和(Ａ,Ｂ)＝等分和(Ｂi,Ｃi)＝等分和(Ｃ,Ｄ)
  となっている。

それゆえ
　Ａ、［Ｂi、］Ｃの和もＢ、［Ｃi、］Ｄの和の、
　ＡがＢの《約数》[等分]または《約数》[等分]和であるのと同じ
　　《約数》[等分]または《約数》[等分]和である。

• 命題７ー５（和も同じ等分）、
  命題７ー６（和も同じ等分和）
  による。
• 　ΣＢi：ΣＣi＝Ａ：Ｂ＝ｎ：ｍ
  となっている。

よって
　ＡがＢに対するように、
　Ａ、Ｃの和がＢ、Ｄの和に対する。

• 定義７ー２１（比例）
  による。

これが証明すべきことであった。

• 命題７ー１２は、
  　Ａ：Ｂ＝Ｂi：Ｃi＝Ｃ：Ｄ＝ｎ：ｍ
  ならば
  　ΣＢi：ΣＣi＝Ａ：Ｂ＝ｎ：ｍ
  のことである。
  
• 命題７ー１２は推論用命題である。

  前提	作図	推論
  定義		7-21
  公準
  公理
  命題	7-11補	7-5,7-6
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭