ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー６（和も同じ等分和）
同じ等分和, (構成.同じ等分和となる第３、４数)
もし
　ある数がある数の《約数》[等分]和であり、
　別のある数が別のある数の
　同じ《約数》[等分]和であるならば、
　１つが１つのいかなる《約数》[等分]和であろうと、
　和も同じ《約数》[等分]和であろう。

• 数は、 定義７ー２ による。
• 等分和は、 定義７ー４ による。
• 同じ等分和 とは、
  　定義の補足（命題７ー５） にいう
  　同じ等分について、
  　同じ個数分である
  すなわち、
  　ＡがＢの等分和であり、
  　ＣがＤの同じ等分和であるとは、
  　ＡがＢの等分(ｍ等分)のｎ個分であり、
  　ＣがＤの同じ等分(ｍ等分)のｎ個分である
  ことである。
  したがって、
  　Ａ、Ｃが同じ等分和ならば
  　それぞれの同じ等分(ｎ等分)のｍ個分Ｂ、Ｄに対して
  　同じ比
  　Ａ：Ｂ＝Ｃ：Ｄ＝ｎ：ｍ
  をもつ。
  （以下、定義の補足（命題７ー６） (同じ等分和)という。）
  

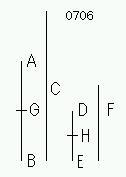
数ＡＢが数Ｃの《約数》[等分]和であるとし、
　ＡＢがＣのいかなる《約数》[等分]和であろうと、
　別の数ＤＥが別の数Ｆの
　同じ《約数》[等分]和であるとせよ。

• 「数（について）・・・とせよ」は、
  　コメント４（命題７ー１） 参照のこと。
  　図は、８、１２、４、６による。
  
• 　数Ｃと
  　Ｃの等分和ＡＢ
  について、
  　数ＤＥ、Ｆを、
  　ＤＥがＦの同じ等分和になる
  ように取ることができる。
  (以下、命題７ー６の補足２ (構成.同じ等分和となる第３、４数)という。)
  すなわち、　
  　命題７ー２（構成.最大公約数）
  により、
  　最大公約数Ｚ(ＡＢ,Ｃ)
  をとれば、
  　個数ｐ(ＡＢ,Ｚ)
  　個数ｑ(Ｃ,Ｚ)
  が定まり、
  　定義７ー１６（かける） 　任意の数Ｗを
  　ｐ回だけ加えてＤＥ、
  　ｑ回だけ加えてＦ
  とすれば、
  　定義７ー４の補足（等分和・倍数）
  による。
  
• 　数Ｃと
  　ＡＢ;等分和(ＡＢ,Ｃ)
  に対して、
  　(数ＤＥ、Ｆ)(;;等分和(ＤＥ,Ｆ)＝等分和(ＡＢ,Ｃ))
  をとっている。　
  

ＡＢ、ＤＥの和も
　Ｃ、Ｆの和の、
　ＡＢがＣの《約数》[等分]和であるのと
　同じ《約数》[等分]和である
　と主張する。
　
ＡＢがＣのいかなる《約数》[等分]和であろうと、
　ＤＥもＦの同じ《約数》[等分]和であるから、

• 命題の設定 による。
• 　等分和(ＡＢ,Ｃ)＝等分和(ＤＥ,Ｆ)＝ｎ／ｍ
  となっている。

　 ＡＢのなかにある
　Ｃの《約数》[等分数]と同じ個数の、
　Ｆの《約数》[等分数]がＤＥのなかにもある。 【・・・(1)】

• 定義の補足（命題７ー６）(同じ等分和)
  による。
• 　個数(ＡＢ,等分Ｚ(ＡＢ,Ｃ).Ｃ)＝個数(ＤＥ,等分Ｚ.Ｆ)
  となっている。

ＡＢがＣの《約数》[等分数]ＡＧ[＝Ｇ1Ｇ'1、ＧiＧ'i、ＧnＧ'n＝]ＧＢに、
　ＤＥがＦの《約数》[等分数]ＤＨ[＝Ｈ1Ｈ'1、ＨiＨ'i、ＨnＨ'n＝]ＨＥに
　分けられたとせよ。

• 約数の個数を２個として
  　推論しようとしている。
  準一般的な証明である。
  コメント２（命題５ー１）参照のこと
  
• 　ＡＢ＝Σ(ＧiＧ'i;等分(ＡＧ,Ｃ).Ｃ)、
  　ＤＥ＝Σ(ＨiＨ'i;等分(ＡＧ,Ｃ).Ｆ)
  となっている。

そうすれば
　ＡＧ[＝Ｇ1Ｇ'1、ＧiＧ'i、ＧnＧ'n＝]ＧＢの個数は
　ＤＨ[＝Ｈ1Ｈ'1、ＨiＨ'i、ＨnＨ'n＝]ＨＥの個数に等しいであろう。

• (1)による。
• 　個数(ＧiＧ'i)＝個数(ＨiＨ'i)
  となっている。

そして
　ＡＧがＣのいかなる《約数》[等分]であろうと、
　ＤＨもＦの同じ《約数》[等分]であるから、

• 定義の補足（命題７ー６）(同じ等分和)
  による。
• 　等分(ＡＧ,Ｃ)＝等分(ＤＨ,Ｆ)
  となっている。

　ＡＧがＣのいかなる《約数》[等分]であろうと、
　ＡＧ、ＤＨの和も
　Ｃ、Ｆの和の同じ《約数》[等分]である。

• 命題７ー５（和も同じ等分）
  による。
• 　等分(ＡＧ,Ｃ)＝等分(ＡＧ＋ＤＨ,Ｃ＋Ｆ)
  となっている。

同じ理由で
　［ＧiＧ'iがＣのいかなる《約数》[等分]であろうと、
　ＧiＧ'i、ＨiＨ'iの和も
　Ｃ、Ｆの和の同じ《約数》[等分]であり、］
　ＧＢがＣのいかなる《約数》[等分]であろうと、
　ＧＢ、ＨＥの和も
　Ｃ、Ｆの和の同じ《約数》[等分]である。

• 　等分(ＧiＧ'i,Ｃ)＝等分(ＧiＧ'i＋ＨiＨ'i,Ｃ＋Ｆ)
  　等分(ＧＢ,Ｃ)＝等分(ＧＢ＋ＨＥ,Ｃ＋Ｆ)
  となっている。

それゆえ
　ＡＢがＣのいかなる《約数》[等分]和であろうと、
　ＡＢ、ＤＥの和も
　Ｃ、Ｆの和の同じ《約数》[等分]和である。

• 公理の補足３（命題５ー１）(１対１対応)、
  定義の補足（命題７ー６） (同じ等分和)
  による。
• 　等分和(ＡＢ,Ｃ)＝等分和(ＡＢ＋ＤＥ,Ｃ＋Ｆ)
  となっている。

これが証明すべきことであった。

• 命題７ー６は、
  　数Ｃ
  に対して、
  　ＡＢ;等分和(ＡＢ,Ｃ)
  　数(ＤＥ、Ｆ)(;;等分和(ＤＥ,Ｆ)＝等分和(ＡＢ,Ｃ))
  をとれば、
  　等分和(ＡＢ,Ｃ)＝等分和(ＡＢ＋ＤＥ,Ｃ＋Ｆ)
  すなわち、　
  　ＡＢ＝ｎＣ／ｍ、ＤＥ＝ｎＦ／ｍ
  ならば
  　ＡＢ＋ＤＥ＝ｎ(Ｃ＋Ｆ)／ｍ
  　のことである。
• 命題７ー６の補足２ (構成.同じ等分和となる第３、４数)

  前提	作図	推論
  定義		7-4補, 7-16
  公準
  公理
  命題		7-2
  その他

• 命題７ー６は推論用命題である。

  前提	作図	推論
  定義		補(題7-6)
  公準
  公理		補3(題5-1)
  命題	7-6補2	7-5
  その他		コ2(題5-1)

前 　　 次 　　 目次 　　頁頭