ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー１０（同じ等分和のいれかえ）
もし
ある数がある数の《約数》[等分]和であり、
別のある数が
　別のある数の同じ《約数》[等分]和であるならば、
いれかえて
第１の数が
　第３の数の
　いかなる《約数》[等分]和または《約数》[等分]であろうと
第２の数も
　第４の数の
　同じ《約数》[等分]和または《約数》[等分]であろう。

• 数は、 定義７ー２による。
• 《約数》[等分]和は、 定義７ー４による。
• 同じ《約数》[等分]和は、 定義の補足（命題７ー６）による。
• いれかえは、 定義の補足（命題７ー９） による。
• 《約数》[等分は、 定義７ー３による。
• 同じ《約数》[等分]は、 定義の補足（命題７ー５）による。

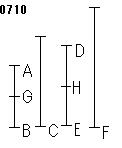
数ＡＢを数Ｃの《約数》[等分]和とし、
別の数ＤＥを
　別の数Ｆの同じ《約数》[等分]和とせよ。

• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１） 参照。
  図は、
  ＡＢが６、Ｃが９、ＤＥが８、Ｆが１２による。
  　命題７ー６の補足２ (構成.同じ等分和となる第３、４数)
  による。
• 　数Ｃ、
  　数ＡＢ[;;等分和(ＡＢ,Ｃ)＝ｎ／ｍ]
  に対して、
  　数ＤＥ、Ｆ
  を
  　等分和(ＡＢ,Ｃ)＝等分和(ＤＥ,Ｆ)＝ｎ／ｍ
  となるようにとる。
  

いれかえて
ＡＢが
　ＤＥのいかなる《約数》[等分]和または《約数》[等分]であろうと、
Ｃも
　Ｆの同じ《約数》[等分]和または《約数》[等分]和である
と主張する。

ＡＢが
Ｃのいかなる《約数》[等分]和であろうと、
ＤＥも
Ｆの同じ《約数》[等分]和であるから、

• 命題の設定による。
• 　等分和(ＡＢ,Ｃ)＝等分和(ＤＥ,Ｆ)＝ｎ／ｍ
  となっている。

ＡＢのなかにある
　Ｃの《約数》[等分数]と同数の、
Ｆの《約数》[等分数]がＤＥのなかにもある。

• 同じ等分和の定義
  定義の補足（命題７ー６）(同じ等分和)
  による。
• 　個数(ＡＢ,等分(Ｃ;;＝Ｃ／ｍ))
  　＝個数(ＤＥ,等分(Ｆ;;＝Ｆ／ｍ))＝ｍ
  となっている。

ＡＢがＣの等分ＡＧ［＝Ｇ1Ｇ'1、ＧiＧ'i、ＧmＧ'm＝］ＧＢに、
ＤＥがＦの等分ＤＨ［＝Ｈ1Ｈ'1、ＨiＨ'i、ＨmＨ'm＝］ＨＥに
分けられたとせよ。
[......(ａ)]

• 　準一般的な証明である。
  　コメント２（命題５ー１）
  　参照のこと。
  　準一般的な証明の一般化の方法は、
  　コメント５（命題５ー１）
  　参照のこと。
  
• 　ＡＢ＝ΣＧiＧ'i、
  　ＤＥ＝ΣＨiＨ'i
  となっている。

そうすれば
ＡＧ［＝Ｇ1Ｇ'1、ＧiＧ'i、ＧmＧ'm＝］ＧＢの個数は
ＤＨ［＝Ｈ1Ｈ'1、ＨiＨ'i、ＨmＨ'm＝］ＨＥの個数に
等しいであろう。

• 同じ等分和の定義
  定義の補足（命題７ー６）(同じ等分和)
  による。
• 　個数(Ｇ1Ｇ'1、ＧiＧ'i、ＧmＧ'm)
  　＝個数(Ｈ1Ｈ'1、ＨiＨ'i、ＨmＨ'm)＝ｍ
  となっている。

そして
ＡＧがＣのいかなる《約数》[等分]であろうと、
ＤＨもＦの同じ《約数》[等分]であり、

• 同じ等分和の定義
  定義の補足（命題７ー６）(同じ等分和)
  による。
• 　等分(ＡＧ,Ｃ)＝等分(ＤＨ,Ｆ)＝１／ｍ
  となっている。

いれかえて

• 定義の補足（命題７ー９）(いれかえ)
  による。

ＡＧがＤＨの
　いかなる《約数》[等分]または《約数》[等分]和であろうと、
ＣもＦの
　同じ《約数》[等分]または《約数》[等分]和である。

• 命題７ー９（同じ等分のいれかえ）
  による。
• 　等分和(ＡＧ,ＤＨ)＝等分和(Ｃ,Ｆ)＝ｑ／ｐ
  となっている。

同じ理由で
［ＧiＧ'i、］ＧＢが［ＨiＨ'i、］ＨＥの
　いかなる《約数》[等分]または《約数》[等分]和であろうと、
ＣもＦの
　同じ《約数》[等分]または《約数》[等分]和である。

• 命題７ー９（同じ等分のいれかえ）
  による。
• 　等分和(ＧiＧ'i,ＨiＨ'i)＝等分和(ＧＢ,ＨＥ)
  　＝等分和(Ｃ,Ｆ)＝ｑ／ｐ
  となっている。

よって
ＡＢがＤＥの
　いかなる《約数》[等分]または《約数》[等分]和であろうと、
ＣもＦの
　同じ《約数》[等分]または《約数》[等分]和である。

• （ａ）により、
  ＡＢはＡＧ、［ＧiＧ'i、］ＧＢの和であり
  ＤＥはＤＨ、［ＨiＨ'i、］ＨＥの和であって、
  命題７ー５（和も同じ等分）、
  命題７ー６（和も同じ等分和）
  により、
  和も同じ等分（和）となることによる。
• 　等分和(ＡＢ,ＤＥ)＝等分和(ΣＧiＧ'i,ΣＨiＨ'i)
  　＝等分和(Ｃ,Ｆ)＝ｑ／ｐ
  となっている。

これが証明すべきことであった。

• 命題７ー１０は、
  　等分和(Ａ,Ｂ)＝等分和(Ｄ,Ｅ)＝ｎ／ｍ
  ならば、
  　等分和(Ａ,Ｄ)＝等分和(Ｂ,Ｅ)＝ｑ／ｐ
  すなわち、
  　Ａ＝ｎＢ／ｍ、Ｄ＝ｎＥ／ｍ、Ａ＝ｑＤ／ｐ
  ならば
  　Ｂ＝ｑＥ／ｐ
  のことである。
  
• 命題７ー１０は推論用命題である。

  前提	作図	推論
  定義		補(題7-6),補(題7-9)
  公準
  公理
  命題	7-6補2	7-5,7-6,7-9
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭