ユークリッド原論をどう読むか（９520）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー２０（等間隔項の大等小）
もし
　３つの量と
　それらと同じ個数の別の量とがあって、
　２つずつとられたとき
　同じ比をなすならば、
　等間隔比により
　第１が第３より大きいならば、
　第４は第６より大きく、
　等しければ、等しく、
　小さければ、小さいであろう。

• 量は、定義５ー１の補足 による。
• 個数は、定義５ー１７の補足 による。
• 同じ比は、定義５ー５ による。
• 等間隔比は、定義５ー１７ による。
• 大きいは、公理１ー８ による。
• 等しいは、公理１ー７ による。
• 小さいは、公理１ー８の補足 による。

　

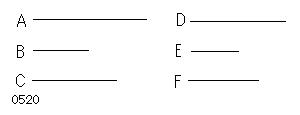
３つの量Ａ、Ｂ、Ｃと
　それらと同じ個数の別の量Ｄ、Ｅ、Ｆとがあり、
　２つずつとられたとき
　同じ比をなす、
　すなわち
　ＡがＢに対するように、
　ＤがＥに対し、
　ＢがＣに対するように、
　ＥがＦに対し、
　ＡがＣより大きいとせよ。

• 同じ比をもつ線分の作図（仮想的）は、
  　コメント２（命題５ー４）参照のこと
• 　量Ａ、Ｂ、Ｄ
  に対して、
  　Ｃ[;;Ａ＞Ｃ]、
  　Ｅ[;;Ａ：Ｂ＝Ｄ：Ｅ]、
  　Ｆ[;;Ｂ：Ｃ＝Ｅ：Ｆ]
  をとっている。

等間隔比により
　ＤもＦより大きく、
　等しければ、等しく、
　小さければ、小さいであろう
　と主張する。
　
ＡはＣより大きく、
　Ｂは別の量であり、

• 命題の設定 による。
• 　Ａ＞Ｃ
  となっている。

　そして
　大きい量は同一の量に対し、
　小さい量より大きい比をもつ
から、

• 命題５ー８（量の大小と比の大小）
  のことである。

　ＡはＢに対し、
　ＣがＢに対するより大きい比をもつ。
【・・・(1)】

• 命題５ー８（量の大小と比の大小）
  による。
• 　Ａ：Ｂ＞Ｃ：Ｂ
  となっている。

ところが
　ＡがＢに対するように、
　ＤがＥに対し、

• 命題の設定 による。
• 　Ａ：Ｂ＝Ｄ：Ｅ
  となっている。

　逆に
　ＣがＢに対するように、
　ＦがＥに対する。
【・・・(2)】

• 命題の設定 命題５ー７の系(比例すれば逆も比例)
  による。
• 　Ｃ：Ｂ＝Ｆ：Ｅ
  となっている。

それゆえ
　ＤはＥに対し、
　ＦがＥに対するより大きい比をもつ。【・・・(3)】

• 命題の設定 (1) (2) 命題５ー１３（大きい比に同じ比は大きい）
  による。
• 　Ｄ：Ｅ＞Ｆ：Ｅ
  となっている。

ところが
　同一の量に対し比をもついくつかの量のうち、
　大きい比をもつ量は大きい。

• 命題５ー１０（比の大小と量の大小）
  のことである。

ゆえに
　ＤはＦより大きい。

• (3) 命題５ー１０（比の大小と量の大小）
  による。
• 　Ｄ＞Ｆ
  となっている。

　
　 同様にしてもし
　ＡがＣに等しければ、
　ＤもＦに等しく、
　小さければ、小さいであろう
　ことを証明しうる。

• 　Ａ(＝、＜)Ｃ
  ならば、
  　Ｄ(＝、＜)Ｆ
  となっている。

よってもし
　３つの量と
　それらと同じ個数の別の量とがあって、
　２つずつとられたとき同じ比をなすならば、
　等間隔比により
　第１が第３より大きいならば、
　第４は第６より大きく、
　等しければ、等しく、
　小さければ、小さいであろう。
これが証明すべきことであった。
　

• 命題５ー２０は、
  　Ａ：Ｂ：Ｃ＝Ｄ：Ｅ：Ｆ、
  　Ａ(＜、＝、＞)Ｃ
  ならば、
  　Ｄ(＜、＝、＞)Ｆ
  のことである。
• 命題５ー２０は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題		5-7系,5-8,5-10,5-13
  その他		コ2(題5-4)

前 　　 次 　　 目次 　　頁頭