ユークリッド原論をどう読むか(9513)
頁末
前
次
目次
ユークリッド原論
第5巻
命題5ー13(大きい比に同じ比は大きい)
(大きい比より大きい比は大きい)
(小さい比に同じ比は小さい)
(小さい比より小さい比は小さい)
(異なる比に同じ比は異なる)
もし
第1の量が第2に対し、
第3が第4に対すると同じ比をもち、
第3が第4に対し、
第5が第6に対するより大きい比をもつ
ならば、
第1は第2に対し、
第5が第6に対するより大きい比をもつであろう。
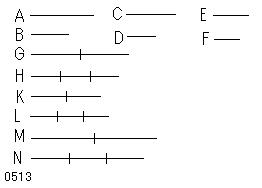
第1の量Aが
第2のBに対し、
第3のCが第4のDに対すると
同じ比をもち、
第3のCが
第4のDに対し、
第5のEが第6のFに対するより
大きい比をもつようにせよ。
-
同じ比をもつ線分の作図(仮想的)は
コメント2(命題5ー4)参照のこと。
-
命題の補足(定義5ー2)(作図.倍量)
により量の倍を作図することで、
A:B、C:D、E:F'が
同じ比をもつようにし、
命題5ー8(量の大小と比の大小)
により、
F'より小さいFを作図する。
-
A:B=C:D
C:D>E:F
をとっている。
第1のAが
第2のBに対し、
第5のEが第6のFに対するより
大きい比をもつであろう
と主張する。
C、Eの《任意の》[ある]同数倍と
D、Fの別の《任意の》[ある]同数倍とがあり、
Cの倍量がDの倍量より大きく、
Eの倍量がFの倍量より大きくない
ようにすることができるから、
そのような倍量がとられたとし、
C、Eの同数倍をG、Hとし、
D、Fの別の《任意の》[ある]同数倍をK、Lとし、
GがKより大きく、
HがLより大きくないとせよ。【・・・(a)】
そして、
GがCの何倍であろうと、
MもAの同じ倍数であり、
KがDの何倍であろうと、
NもBの同じ倍数である
ようにせよ。【・・・(b)】
- 推論の設定である。
- 量の倍は、命題の補足(定義5ー2)(作図.倍量)
による。
-
M=倍数(G,C)×A=mA、
N=倍数(K,D)×B=nB
をとっている。
そうすれば、
AがBに対するように、
CがDに対し、
- 命題の設定
による。
-
A:B=C:D
となっている。
そして
A、Cの同数倍M、Gと、
B、Dの別の《任意の》[ある]同数倍N、Kがとられたから、
もし
MがNより大きければ、
GもKより大きく、
等しければ、
等しく、
小さければ、
小さい。【・・・(1)】
- 定義5ー5(同じ比)
による。
-
M(;=mA)(<、=、>)N(;=nB)
ならば、
G(;=mC)(<、=、>)K(;=nD)
となっている。
ところが
GはKより大きい。
- (a)
による。
-
G(;=mC)>K(;=nD)
となっている。
それゆえ
MもNより大きい。
- (1)
によれば、
MがNより大きければ、
GもKより大きいということで、
その逆ではない。
しかし、
命題5ー11の補足(同じ比は互いに同じ)
により、
GがKより大きければ、
MもNより大きいことがわかる。
-
M(;=mA)>N(;=nB)
となっている。
ところが
HはLより大きくない。
- (a)
による。
-
H(;=mE)<=L(;=nF)
となっている。
そして
M、HはA、Eの同数倍、
N、LはB、Fの別の《任意の》[ある]同数倍である。
- (b)
による。
- 《任意の》[ある]は、コメント2(命題5ー8)参照のこと。
-
倍数(M,A)=倍数(H,E)=m、
倍数(N,B)=倍数(L,F)=n
となっていて、
さきに、
M(;=mA)>N(;=nB)
H(;=mE)<=L(;=nF)
となっていた。
ゆえに
AはBに対し
EがFに対するより
大きい比をもつ。
- 定義5ー5(同じ比)
による。
-
A:B>E:F
となっている。
よってもし
第1の量が第2に対し、
第3が第4に対すると
同じ比をもち、
第3が第4に対し、
第5が第6に対するより
大きい比をもつならば、
第1は第2に対し、
第5が第6に対するより
大きい比をもつであろう。
これが証明すべきことであった。
-
大きい比より大きい比は大きい。
以下、命題5ー13の補足(大きい比より大きい比は大きい)という。
A:B>C:D、C:D>E:Fとする。
定義5ー7(大きい比)
により
ある倍数(個数)m、m'があって、
mA>m'BかつmC<=m'D
また、
ある倍数n、n'があって、
nC>n'DかつnE<=n'F
定義の補足(公理1ー5)(同じもののn倍)、
公理1ー4の補足3(大きい(小さい)ものどうしを加える)
により
mn'A>m'n'Bかつmn'C<=m'n'D
m'nC>m'n'Dかつm'nE<=m'n'F
【・・・(2)】
ここで、
mn'C<=m'n'D、
m'nC>m'n'Dであるから
m'nはmn'より大きい倍数であるので、
m'nA>mn'A。
mn'A>m'n'Bであったから
公理1ー8の補足3(大きい・小さいものより大きい・小さい)
により
m'nA>m'n'B。
また(2)
より
m'nE<=m'n'F
したがって、
定義5ー7(大きい比)
より
A:B>E:F
- 命題5ー13の補足は、
A:B>C:D、C:D>E:F
なら
A:B>E:F
のことである。
-
小さい比に同じ比は小さい
(以下、命題5ー13の補足2(小さい比に同じ比は小さい)という。)
ことがわかる。
A:B<C:D、
A:B=E:F
とする。
背理法の仮定として、
E:F=C:D
とすると、
命題5ー11(同一の比に同じ比)、
により
A:B=C:D
となって前提に矛盾する。
また、
背理法の仮定として、
E:F>C:D
とすると、
本命題5ー13(大きい比に同じ比は大きい)
により、
A:B>C:D
となって前提に矛盾する。
背理法により、
¬(E:F=C:D)、
¬(E:F>C:D)、
公理の補足3(定義5ー7)(比は等か大か小)
により
E:F<C:D
となる。
同様に
小さい比より小さい比は小さい。
(以下、命題5ー13の補足3(小さい比より小さい比は小さい)という。)
A:B<C:D、
E:F<A:B
とする。
背理法の仮定として、
E:F=C:D
とすると、
命題5ー13(大きい比に同じ比は大きい))、
により
A:B<E:F
となって前提に矛盾する。
また、
背理法の仮定として、
E:F>C:D
とすると、
命題5ー13の補足(大きい比より大きい比は大きい)
により、
A:B<E:F
となって前提に矛盾する。
背理法により、
¬(E:F=C:D)、
¬(E:F>C:D)、
公理の補足3(定義5ー7)(比は等か大か小)
により
E:F<C:D
となる。
また、
本命題5ー13(大きい比に同じ比は大きい)、
命題5ー13の補足2(小さい比に同じ比は小さい)、
公理の補足3(定義5ー7)(比は等か大か小)
により、
異なる比に同じ比は異なる。
(以下、命題5ー13の補足4(異なる比に同じ比は異なる)という。)
- 命題5ー13は、
A:B=C:D、C:D>E:F
なら
A:B>E:Fのことである。
-
命題5ー13の補足(大きい比より大きい比は大きい)は推論用命題である。
-
命題5ー13の補足2(小さい比に同じ比は小さい)
-
命題5ー13の補足3(小さい比より小さい比は小さい)
-
命題5ー13の補足4(異なる比に同じ比は異なる)
- 命題5ー13は推論用命題である。
前
次
目次
頁頭
