ユークリッド原論をどう読むか(9521)
頁末
前
次
目次
ユークリッド原論
第5巻
命題5ー21(乱比例の等間隔項の大等小)
もし
3つの量と
それらと同じ個数の別の量とがあり、
2つずつとられたとき同じ比をなし、
それらの比例が《いれかえれる》[乱比例]ならば、
等間隔比により
第1が第3より大きければ、
第4も第6より大きく、
等しければ、等しく、
小さければ、小さいであろう。
- 量は、定義5ー1の補足
による。
- 個数は、定義5ー17の補足
による。
- 同じ比は、定義5ー5
による。
- 比例は、定義5ー6
による。
- 乱比例は、定義5ー18
による。
中村他訳の原論においては、
錯比と乱比例が
ともに
「いれかえて」と
同じ動詞で表現されているが
Euclid's Elements
(Clark University Professor D.E.Joyceの
http://aleph0.clarku.edu/~djoyce/java/elements/elements.html)
においては、
錯比は、
they are also proportional alternately
というように表現され、
乱比例は、
the proportion of them is perturbed
というように表現され、
明確に区別される。
- 等間隔比は、定義5ー17
による。
- 大きいは、公理1ー8
による。
- 等しいは、公理1ー7
による。
- 小さいは、公理1ー8の補足
による。
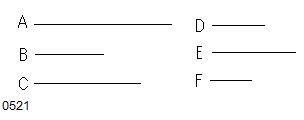
3つの量A、B、Cと
それらと同じ個数の別の量D、E、Fとがあり、
2つずつとられたとき
同じ比《をなすとし》[であり]、
それら《の比例がいれかえれ、》
[が乱比例をなし、]
すなわちAがBに対するように、
EがFに対し、
BがCに対するように
DがEに対し、
AがCより大きいとせよ。
-
Euclid's Elements
(Clark University Professor D.E.Joyceの
http://aleph0.clarku.edu/~djoyce/java/elements/elements.html)
においては、
・・・,
which taken two and two are in the same ratio,
and let the proportion of them be perturbed,
so that ・・・
となっている。
- 同じ比をもつ線分の作図(仮想的)は、
コメント2(命題5ー4)参照のこと。
-
量A、B、E
に対して、
C[;;A>C]、
F[;;A:B=E:F]、
D[;;B:C=D:E]
をとっている。
等間隔比により
DもFより大きく、
[AがCに]等しければ、
[DもFに]等しく、
[AがCより]小さければ、
[DもFより]小さいであろう
と主張する。
AはCより大きく、
Bは別の量であるから、
AはBに対し、
CがBに対するより
大きい比をもつ。【・・・(1)】
- 命題5ー8
(量の大小と比の大小)
による。
-
A:B>C:B
となっている。
ところが
AがBに対するように、
EがFに対し、
逆に
CがBに対するように、
EがDに対する。
それゆえ
EがFに対し、
EがDに対するより
大きい比をもつ。【・・・(2)】
しかも
同一の量が
それに対して
大きい比をもつ量は小さい。
ゆえに
FはDより小さい。
したがって
DはFより大きい。
同様にしてもし
AがCに等しければ、
DもFに等しく、
小さければ、小さい
であろうことを証明しうる。
-
A(=、<)C
ならば、
D(=、<)C
となっている。
よってもし
3つの量と
それらと同じ個数の別の量とがあり、
2つずつとられたとき
同じ比をなし、
それらの比例が《いれかえれる》[乱比例]ならば、
等間隔比により
第1が第3より大きければ
第4も第6より大きく、
等しければ、等しく、
小さければ、小さいであろう。
これが証明すべきことであった。
- 命題5ー21は、
A:B=E:F、
B:C=D:E
において、
A<=>C
ならば、
D<=>F
ということである。
- 命題5ー21は推論用命題である。
前
次
目次
頁頭
