ユークリッド原論をどう読むか（７）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー３０（作図.弧の２等分）
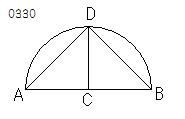
与えられた弧を
　２等分すること。

• 弧は、 定義１ー１８の補足 による。
• 等分は、 定義の補足２（公理１ー６） による。

与えられた弧を
　ＡＤＢとせよ。

• 　円ＡＤＢ[]
  に対して、
  　点Ａ[上.円ＡＤＢ]、
  　点Ｂ[上.円ＡＤＢ,外.Ａ]、
  　点Ｄ[上.円ＡＤＢ,外.Ａ,外Ｂ]、
  　弧ＡＤＢ
  をとっている。

このとき
　弧ＡＤＢを
　２等分しなければならぬ。


ＡＢが結ばれ、

• 公準１ー１ （作図.直線）
  による。
• 　線分ＡＢ
  をとっている。

　Ｃにおいて２等分され、

• 命題１ー１０ （作図・線分の２等分）
  による。
• 　中点(ＡＢ)
  をとっている。

　点Ｃから
　弦ＡＢに直角にＣＤがひかれ、 【・・・(a)】

• 命題１ー１１ （作図・線分からの垂線）
  による。
• 　交点Ｄ(弦ＡＤＢ,垂線(Ｃ,ＡＢ))
  をとっている。
  

　ＡＤ、ＤＢが結ばれたとせよ。

• 公準１ー１ （作図.直線）
  による。
• 　線分ＡＤ、ＤＢ
  をとっている。

そうすれば
ＡＣは
　ＣＢに等しく、

• (a) による。
• 　ＡＣ＝ＣＢ
  となっている。

ＣＤが
　共通であるから、
２辺ＡＣ、ＣＤは
　２辺ＢＣ、ＣＤに等しい。

• 　前節による。
• 　(ＡＣ、ＣＤ)＝(ＢＣ、ＣＤ)
  となっている。

そして
角ＡＣＤは
　角ＢＣＤに等しい。
なぜなら
　双方とも直角であるから。

• (a) による。
• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６） を参照のこと。
• 　∠ＡＣＤ＝∠ＢＣＤ＝∠Ｒ
  となっている。

それゆえ
底辺ＡＤは
　底辺ＤＢに等しい。

• 命題１ー４ （２辺挟角相等）
  による。
• 　ＡＤ＝ＤＢ
  となっている。

ところが
等しい弦は
　等しい弧を切り取る。
すなわち
　切り取られた
大きい弧は
　大きい弧に、
小さい弧は
　小さい弧に
　等しい。

• 命題３ー２８ （等しい弦は等しい弧を切り取る）
  による。

そして
弧ＡＤ、ＤＢの双方は
　半円より小さい。

• 命題３−１の系 (中心は弦の２等分線上)
  により、
  中心は
  　直線ＣＤ上にある。
  したがって
  弧の双方は
  　それぞれ
  　直径の異なる一方の側にある。
  よって
  双方の弧は
  　半円より小さい。
  すなわち、
  　 命題３ー２８ （等しい弦は等しい弧を切り取る）
  にいう
  　小さい弧である。
• 　弧ＡＤ;弧(上.円ＡＤＢ,反対側(ＡＤ,中心.円ＡＤＢ))
  　弧ＤＢ;弧(上.円ＡＤＢ,反対側(ＤＢ,中心.円ＡＤＢ))
  となっている。

ゆえに
弧ＡＤは
　弧ＤＢに等しい。

• 　前節、前々節による。
• 　弧ＡＤ≡弧ＤＢ
  となっている。

よって
与えられた弧は
　点Ｄにおいて２等分された。
これが作図すべきものであった。

• 命題３ー３０は、
  　弧ＡＤＢ[]
  に対して、
  　中点Ｃ(弦ＡＢ)、
  　交点Ｄ(弧ＡＤＢ,垂線(Ｃ,ＡＢ))
  をとれば、
  　弧ＡＤ≡弧ＤＢ
  のことである。
  
• 命題３ー３０は作図用命題である。

  前提	作図	推論
  定義
  公準	1-1
  公理
  命題	1-10 , 1-11	1-4 , 3-1系 , 3-28
  その他		コ2(題1-16)f

前 　　 次 　　 目次 　　頁頭