ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー１４（等しい弦と中心からの距離）
円において
　等しい弦は
　中心から等距離にあり、
　中心から等距離にある
　　弦は
　また互いに等しい。
　
ＡＢＣＤを円、
　ＡＢ、ＣＤを
　　それにおける等しい弦とせよ。

• 　円ＡＢＣＤ
  に対して、
  　弦ＡＢ.円ＡＢＣＤ、
  　点Ｃ[円ＡＢＣＤ]、
  　交点Ｄ[円ＡＢＣＤ,円(Ｃ,ＡＢ)]
  　弦ＣＤ.円ＡＢＣＤ
  をとっている。
  　ＡＢ＝ＣＤ
  となっている。

ＡＢ、ＣＤは
　中心から等距離にある
　と主張する。


　
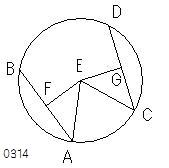
円ＡＢＣＤの
　中心がとられ、
　それをＥとし、

• 命題３ー１（作図.円の中心） による。
• 　中心Ｅ,円ＡＢＣＤ
  をとっている。

　ＥからＡＢ、ＣＤに
　垂線ＥＦ、ＥＧがひかれ、 【・・・(a)】

• 命題１ー１１作図・線分からの垂線） による。
• 　垂線ＥＦ(Ｅ,ＡＢ;;Ｆ;上.ＡＢ)、
  　垂線ＥＧ(Ｅ,ＣＤ;;Ｇ;上.ＣＧ)、
  をとっている。

　ＡＥ、ＥＣが結ばれたとせよ。

• 公準１ー１（作図.直線） による。
• 　線分ＡＥ、ＥＣ
  をとっている。

そうすれば
　中心を通る線分ＥＦは
　中心を通らない弦ＡＢと
　直角に交わり、
　それを
　また
　２等分する。

• 　ＡＢ（通）中心.円ＡＢＣＤ
  ならば
  　ＡＢ;直径.円ＡＢＣＤ、
  　ＣＤ＝ＡＢ
  により
  　ＣＤ;直径.円ＡＢＣＤ
  　ＣＤ（通）中心.円ＡＢＣＤ
  となり、
  　ＡＢ、ＣＤとも、
  　中心からの距離は０で、
  　等しい。
• (a) ,命題３ー３（直径と弦） による。
• 　ＥＦ⊥ＡＢ
  　Ｆ.中点(ＡＢ)
  となっている。

それゆえ
ＡＦはＦＢに等しい。
ゆえに
ＡＢは
　ＡＦの２倍である。

• 定義の補足（公理１ー５）（同じもののｎ倍） による。
• 　ＡＢ;２×ＡＦ
  となっている。

同じ理由で
　ＣＤもＣＧの２倍である。
しかも
ＡＢは
　ＣＤに等しい。

• 命題の設定 である。
• 　ＣＤ＝２×ＣＧ、
  　ＡＢ＝ＣＤ
  となっている。

したがって
ＡＦも
　ＣＧにひとしい。 【・・・(1)】

• 公理１ー６の補足３（等しいもののｎ等分、ｎ等分に等しいもの） による。
• 　ＡＦ＝ＣＧ
  となっている。

そして
ＡＥは
　ＥＣに等しいから、

• (a) ,定義１ー１５（円） による。
• 　ＡＥ＝ＥＣ
  となっている。

ＡＥ上の正方形は
　ＥＣ上の正方形に等しい。

• 定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン） による。
• 　正方(_ＡＥ)＝正方(_ＥＣ)
  となっている。

ところが
　Ｆにおける角は直角であるから、

• (a) による。
• 　∠ＥＦＡ＝∠Ｒ
  となっている。

ＡＦ、ＥＦ上の正方形の和は
　ＡＥ上の正方形に等しい。

• 命題１ー４７（三平方の定理） による。
• 　正方(_ＡＦ)＋正方(_ＥＦ)＝正方(_ＡＥ)
  となっている。

また
　Ｇにおける角も直角であるから

• (a) による。
• 　∠ＣＧＥ＝∠Ｒ
  となっている。

ＥＧ、ＧＣ上の正方形の和も
　ＥＣ上の正方形に等しい。

• 命題１ー４７（三平方の定理） による。
• 　正方(_ＥＧ)＋正方(_ＧＣ)＝正方(_ＥＣ)
  となっている。

それゆえ、
ＡＦ、ＦＥ上の正方形の和は
　ＣＧ、ＧＥ上の正方形の和に等しく、 【・・・(2)】

• 公理１ー１の補足（等しいものに等しい） による。
• 　正方(_ＡＦ)＋正方(_ＥＦ)
  　＝正方(_ＣＧ)＋正方(_ＧＥ)
  となっている。

ＡＦは
　ＣＧに等しいから、

• (1) による。
• 　ＡＦ＝ＣＧ
  となっている。

　そのうち
ＡＦ上の正方形は
　ＣＧ上の正方形に等しい。

• 定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン） による。
• 　正方(_ＡＦ)＝正方(_ＣＧ)
  となっている。

ゆえに
　残りの
ＦＥ上の正方形は
　ＥＧ上の正方形に等しい。

• (2) ,公理１ー３（等しいものから等しいものをひく）
  による。
• 　正方(_ＦＥ)＝正方(_ＥＧ)
  となっている。

したがって
ＥＦは
　ＥＧに等しい。

• 命題１ー４８の補足（正方形の大等小と辺の大等小）
  による。
• 　ＦＥ＝ＥＧ
  となっている。

ところが
　円において
　弦は
　中心からそれにひかれた垂線が等しい時、
　中心から等距離にあるといわれる。

• 定義３ー４（中心から等距離）
  による。

よって、
　ＡＢ、ＣＤは
　中心から等距離にある。

次に
　弦ＡＢ、ＣＤが
　中心から等距離にある、
　すなわち
　ＥＦが
　ＥＧに等しいとせよ。

• 　ＥＦ＝ＥＧ
  となっている。

ＡＢも
　ＣＤに等しい
　と主張する。
同じ作図がなされて、

• (a) である。

　同様にして
ＡＢは
　ＡＦの、
ＣＤは
　ＣＧの２倍である
　ことを証明しうる。 【・・・(3)】

• (a) ,命題３ー３（直径と弦）
  による。
• 　ＡＢ＝２×ＡＦ、
  　ＣＤ＝２×ＣＧ
  となっている。

そして
ＡＥは
　ＣＥに等しいから、

• (a) ,定義１ー１５（円）
  
• 　ＡＥ＝ＣＥ
  となっている。 による。

ＡＥ上の正方形は
　ＣＥ上の正方形に等しい。

• 定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　正方(_ＡＥ)＝正方(_ＣＥ)
  となっている。

ところが
ＥＦ、ＦＡ上の正方形の和は
　ＡＥ上の正方形に等しく、
ＥＧ、ＧＣ上の正方形の和は
　ＣＥ上の正方形に等しい。

• 命題１ー４７（三平方の定理）
  による。
• 　正方(_ＥＦ)＋正方(_ＦＡ)＝正方(_ＡＥ)、
  　正方(_ＥＧ)＋正方(_ＧＣ)＝正方(_ＣＥ)
  となっている。

それゆえ
ＥＦ、ＦＡ上の正方形の和は
　ＥＧ、ＧＣ上の正方形の和に等しく、

• 公理１ー１の補足（等しいものに等しい）
  による。
• 　正方(_ＥＦ)＋正方(_ＦＡ)
  　＝正方(_ＥＧ)＋正方(_ＧＣ)
  となっている。

ＥＦは
　ＥＧに等しいから、

• 命題の設定 である。
• 　ＥＦ＝ＦＧ
  となっている。

　そのうち
ＥＦ上の正方形は
　ＥＧ上の正方形に等しい。

• 定義１ー２２（正方形・矩形・菱形・長斜方形・トラペジオン）
  による。
• 　正方(_ＥＦ)＝正方(_ＥＧ)
  となっている。

ゆえに
　残りの
ＡＦ上の正方形は
　ＣＧ上の正方形に等しい。

• 公理１ー３（等しいものから等しいものをひく）
  による。
• 　正方(_ＡＦ)＝正方(_ＣＧ)
  となっている。

したがって
ＡＦは
　ＣＧに等しい。 【・・・(4)】

• 命題１ー４８の補足（正方形の大等小と辺の大等小）
  による。
• 　ＡＦ＝ＣＧ
  となっている。

そして
ＡＢは
　ＡＦの２倍であり、
ＣＧは
　ＣＤの２倍である。

• (3) による。
• 　ＡＢ＝２×ＡＦ、
  　ＣＧ＝２×ＣＧ
  となっている。

それゆえ
ＡＢは
　ＣＤに等しい。

• (4) , 公理１ー５の補足２ （等しいもののｎ倍、ｎ倍に等しいもの）
  による。
• 　ＡＢ＝ＣＤ
  となっている。

　
よって
　円において
　等しい弦は
　中心から等距離にあり、
　中心から等距離にある弦は
　また
　互いに等しい。
　これが証明すべきことであった。

• 命題３ー１４は、
  　円ＡＢＣＤ
  　中心Ｅ.円ＡＢＣＤ、
  　交点Ｆ(垂線(Ｅ,ＡＢ),ＡＢ)、
  　交点Ｇ(垂線(Ｅ,ＣＤ),ＣＤ)、
  に対して、
  　弦ＡＢ.円ＡＢＣＤ、
  　＝弦ＣＤ.円ＡＢＣＤ、
  ならば、
  　ＥＦ＝ＥＧ。
  逆に、
  　ＥＦ＝ＥＧ、
  ならば、
  　弦ＡＢ.円ＡＢＣＤ、
  　＝弦ＣＤ.円ＡＢＣＤ
  のことである。
• 命題３ー１４は推論用命題である。

  前提	作図	推論
  定義		1-15, 1-22, 補(理1-5), 3-4
  公準	1-1
  公理		1-1補, 1-3, 1-5補2, 1-6補3
  命題	1-11, 3-1	1-47, 1-48補, 3-3
  その他

前 　　 次 　　 目次 　　頁頭