ユークリッド原論をどう読むか（６）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第３巻

命題３ー１３（２円の接点は１つ）
円は
　円と、
　内側で接するにせよ
　外側で接するにせよ、
　一つより多くの点においては
　接しない。

• 円は、 定義１ー１５による。
• 内側は、命題の補足３（定義１ー１４）による。
• 接するは、 定義３ー３による。
• 外側は、命題の補足３（定義１ー１４）による。
• 点は、 定義１ー１による。

［そうでないとすれば、］

• 背理法の仮定が以下に続く。

もし可能ならば、

• 「もし可能ならば」は、
  コメント２(命題１−７）参照のこと。

［命題の設定により、
　２円について、
一方が他方の内部で接する場合と
互いに他方と外部で接する場合
がある。
一方が他方の内部で接する場合 ］
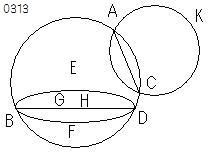
円ＡＢＣＤが
　円ＥＢＦＤと
　まず内側で一つより多くの点
　すなわちＤ、Ｂで
　接するとせよ。
そして
　円ＡＢＣＤの中心Ｇ、
　ＥＢＦＤの中心Ｈ
　がとられたとせよ。 【・・・(a)】

• 命題３ー１（作図.円の中心） による。
• 　円ＡＢＣＤ
  に対して、
  　円ＥＢＦＤ[;;円ＥＢＦＤ;内側.円ＡＢＣＤ]、
  　点Ｄ、Ｂ;接点[円ＥＢＦＤ,円ＡＢＣＤ]、
  　中心Ｇ.円ＡＢＣＤ、
  　中心Ｈ.円ＥＢＦＤ
  をとっている。

そうすれば
　Ｇ、Ｈを結ぶ線分は
　Ｂ、Ｄに落ちるであろう。 【・・・(b)】

• (a) ,命題３ー１１（内接２円の中心と接点） による。
• 　直線ＧＨ;（通）Ｂ、Ｄ
  となっている。

ＢＧＨＤのようになるとせよ。

• 　直線ＧＨ≡直線ＢＧＨＤ
  となっている。

そうすれば
　点Ｇは
　円ＡＢＣＤの中心であるから、
ＢＧは
　ＧＤに等しい。

• 定義１ー１５（円） による。
• 　ＢＧ＝ＧＤ
  となっている。

それゆえ
ＢＧは
　ＨＤより大きい。

• (b) ,公理１ー８（大きい） により、
  　ＧＤはＨＤより大きいことによる。
• 　ＢＧ＞ＨＤ
  となっている。

ゆえに
ＢＨは
　なおさら
　ＨＤより大きい。【・・・(1)】

• (b) , 公理１ー８（大きい） 、 公理１ー８の補足２（等より大・小、大・小に等） により、
  　ＢＨはＢＧより大きいことによる。
• 　ＢＨ＞ＢＧ
  となっている。

また
　点Ｈは円ＥＢＦＤの中心であるから、
ＢＨは
　ＨＤに等しい。

• 定義１ー１５（円） による。
• 　ＢＨ＝ＨＤ
  となっている。

ところが
　それよりなおさら大きい
　ことも先に証明された。

• (1) による。
• 　ＢＨ＞ＨＤ
  となっていた。

これは不可能である。

• 背理法の仮定による矛盾である。

したがって
　円は
　円と内側で
　１つより多くの点で
　接することはない。 【・・・(2)】

• 背理法による。

互いに他方と外部で接する場合
さらに
　外側でも
　［１つより多くの点で］
　接しない
　と主張する。

• 場合分けのもう一方である。

もし可能ならば、

• 背理法の仮定を
  　述べようとしている。
• 「もし可能ならば」は、
  コメント２(命題１−７）参照のこと。

　円ＡＣＫ《か》［が］
　円ＡＢＣＤと
　外側で１つより多くの点、
　すなわちＡ、Ｃで
　接するとし、 【・・・(c)】

• 背理法の仮定である。

　ＡＣが結ばれたとせよ。

• 公準１ー１（作図.直線） による。
• 　円ＡＣＫ[;;円ＡＣＫ;外側.円ＡＢＣＤ]、
  　Ａ、Ｃ;接点[円ＡＣＫ,円ＡＢＣＤ]
  をとったとしている。

そうすれば
　円ＡＢＣＤ、ＡＣＫの
　双方の円周上に
　任意の２点Ａ、Ｃがとられたから、

• 本命題においては、
  　Ａ、Ｃは
  　任意にとられたのではない。
  しかし、
  　Euclid's Elements
  　（Clark University Professor D.E.Joyceの
  　http://aleph0.clarku.edu/~djoyce/java/elements/elements.html）
  においても、
  　「two points A and C have been taken at random」
  　と記載されており、
  　J. L. Heiberg
  　のテキストにおいても
  　そうなっているものと思われる。
  証明の流れに沿うならば、
  　「任意にとられた場合でも」
  　のようであるべきである。
  命題３ー２（弦は円の内部） の表現に
  　あわせたものと思われる。
• 　Ａ、Ｃ;点[円ＡＢＣＤ]、
  　Ａ、Ｃ;点[円ＡＣＫ]
  となっている。

　２点を結ぶ線分は
　双方の内部におちるであろう。

• 命題３ー２（弦は円の内部） による。
• 　線分ＡＣ;内側.円ＡＢＣＤ、
  　線分ＡＣ;内側.円ＡＣＫ
  となっている。

ところが
　それは
　ＡＢＣＤの内部に、
　ＡＣＫの外部におちた。

• (c) ,定義３ー３（相接する） により、
  　円ＡＢＣＤは
  　円ＡＣＫと外側で接するので、
  　内側に円ＡＣＫの内部をもたないから、
  　ＡＢＣＤの内部の
  　　線分ＡＣは
  　ＡＣＫの外部にある
  　ことになるという意味である。
• 　ＡＣ;内側.円ＡＢＣＤ、
  　ＡＣ;外側.円ＡＣＫ
  となっている。

これは
　不合理である。

• 背理法の仮定による矛盾である。

したがって
　円は
　円と外側で
　１つより多くの点では接しない。

• 背理法による。
• 　個数(接点(円,円))≦１
  となっている。

また
　内側ででも接しない
　ことが先に証明された。

• (2) による。

よって
[ ２つの場合の結果により ]
　円は
　円と、
　内側で接するにせよ
　外側で接するにせよ、
　１つより多くの点においては接しない。
［これが証明すべきことであった。］

• 命題３ー６の補足６(接する２円の接点は１つ) で論じたことである。
• 命題３ー１３は、
  　円ＡＢＣＤ
  に対して、
  　円ＥＢＦ[;;接点以外.円ＥＢＦ;内.円ＡＢＣＤ]、
  　円ＡＣ'Ｋ[;;接点以外.円ＡＣ'Ｋ;外.円ＡＢＣＤ]、
  をとれば、
  　個数(接点(円ＡＢＣＤ,円ＥＢＦ))≦１
  　個数(接点(円ＡＢＣＤ,円ＡＣ'Ｋ))≦１
  のことである。
• 命題３ー１３は推論用命題である。

  前提	作図	推論
  定義		1-15,3-3
  公準	1-1
  公理		1-8,1-8補2
  命題	3-1	3-2,3-11
  その他		背理法,コ2(題1-7)、題の場合分け

前 　　 次 　　 目次 　　頁頭