ユークリッド原論をどう読むか(4)
頁末
前
次
目次
ユークリッド原論
第1巻
命題1−45(作図.直線図形,直線角と平行四辺形)
「直線図形の四角形による準一般的証明」
(作図.直線図形,線分,直線角と平行四辺形)
与えられた直線角のなかに
与えられた直線図形に等しい
平行四辺形をつくること。
与えられた直線図形をABCD、
与えられた直線角をEとせよ。
このとき
与えられた角Eのなかに
直線図形ABCDに等しい
平行四辺形をつくらねばならぬ。
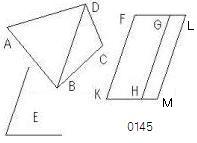
DBが結ばれ、
- 公準1−1(作図.直線)
による。
-
線分DB
をとっている。
三角形ABDに等しい
平行四辺形FHが
Eに等しい角HKFのなかに
つくられたとせよ。
【・・・(a)】
- 命題1−42(作図.線分,三角形,直線角と平行四辺形)
による。
-
半直線KM'、
半直線KF'[∠F'KM'=∠E]、
平四FKHG(K,点H[KM',KH=AB/2],点F[KF',平四FKGH=△ABC]
をとっている。
そして
線分GH上に
三角形DBCに等しい
平行四辺形GMが、
Eに等しい角GHMのなかに
つくられたとせよ。
【・・・(b)】
- 命題1−44(作図.線分,三角形,直線角と平行四辺形)
による。
-
そうすれば
角Eは
角HKF、GHMの双方に等しいから、
角HKFもGHMに等しい。
KHGが
双方に加えられたとせよ。
そうすれば
角FKH、KHGの和は
角KHG、GHMの和に等しい。
ところが
角FKH、KHGの和は
2直角に等しい。
ゆえに
KHG、GHMの和も2直角に等しい。
かくて
任意の線分GHに対し
その上の点Hにおいて
同じ側にない2線分KH、HMが
接角の和を2直角に等しくする。
ゆえに
KHはHMと一直線をなす。
そして
線分HGが
平行線KM、FGに交わるから、
錯角MHG、HGFは
互いに等しい。
双方に
角HGLが加えられたとせよ。
そうすれば
MHG、HGLの和は
角HGF、HGLの和に等しい。
ところが
角MHG、HGLの和は
2直角に等しい。
ゆえに
HGF、HGLの和も
2直角に等しい。
したがって
FGはGLと一直線をなす。
そして
FKはHGに等しくかつ平行であり、
他方
HGもMLに等しくかつ平行であるから、
KFも
MLに等しくかつ平行である。
ゆえに
KFLMは平行四辺形である。
そして
三角形ABDは
平行四辺形FHに、
DBCは
GMに等しいから、
直線図形ABCD全体は
平行四辺形KFLM全体に等しい。
よって
与えられた直線図形ABCDに等しい
平行四辺形KFLMが
与えられた直線角Eに等しい角FKMのなかに
つくられた。
これが作図すべきものであった。
- この命題が、
直線図形を
指定された角におさまる
平行四辺形に
等積変形する最後の一歩である。
-
「直線図形は、
対角線を引くことで三角形に分解されるので、
四角形を題材として
準一般的に証明される。」
(以下、コメント(命題1ー45)(直線図形の四角形による準一般的証明)という。)
-
命題1ー44を踏まえると、
与えられた線分上に
与えられた直線図形に等しい
平行四辺形を
与えられた直線角に等しい
角のなかにつくることができる。
(以下、命題1ー45の補足2(作図.直線図形,線分,直線角と平行四辺形)という。)
- この命題により、
直線図形については、
面積の普遍単位に
ほとんど到着したことになる。
- 命題1ー45の補足2(作図.直線図形,線分,直線角と平行四辺形)
- 命題1-45は作図用命題である。
前
次
目次
頁頭
