ユークリッド原論をどう読むか（４）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１−４４（作図.線分,三角形,直線角と平行四辺形）
与えられた線分上に
　与えられた三角形に等しい
　平行四辺形を
　与えられた直線角に等しい
　角のなかに
　つくること。

• 線分は、定義１−４の補足による。
• 三角形は、定義１−１９の補足２による。
• 平行四辺形は、定義の補足（命題１−３４）による。
• 直線角は、定義１−９による。
• 等しいは、公理１−７による。
• 角は、定義１−８による。

与えられた線分をＡＢ、
　与えられた三角形をＣ、
　与えられた直線角をＤとせよ。

• 　線分ＡＢ、
  　△Ｃ、
  　直線角Ｄ
  をとっている。

このとき
　与えられた線分ＡＢ上に
　与えられた三角形Ｃに
　等しい平行四辺形を
　角Ｄに等しい角のなかに
　つくらねばならぬ。


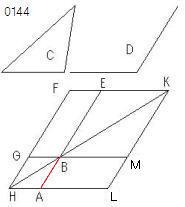
　［ＡＢの延長上にＥをとり、］
　角Ｄに等しい角ＥＢＧのなかに
　三角形Ｃに等しい
　平行四辺形ＢＥＦＧが
　作られた
とせよ。
　　　　　　【・・・(a)】

• 　公準１ー２（作図.直線の延長）
  により、
  　ＡＢをＢの方へ延長して、
  　ＡＥ'とし、
  　ＢＥ'上に、
  　命題１ー２３（作図・直線上に指定された角）
  により、
  　∠Ｄに等しい∠Ｇ'ＢＥ'をとり、
  　命題１−４２（作図.角,三角形と平行四辺形）
  により、
  　∠Ｇ'ＢＥ'の中に、
  　△Ｃに等しい平行四辺形ＢＥＦＧをとる。
  
• 　線分ＡＢ
  に対して、
  　半直線ＢＥ'(延長ＡＢ)、
  　線分ＢＧ'[;;∠Ｇ'ＢＥ'＝∠Ｄ,ＢＧ'＝辺1.△Ｃ]、
  　点Ｅ"(同側(ＢＧ',Ｅ'),△ＢＧ'Ｅ"≡△Ｃ)、
  　中点Ｇ(ＢＧ')、
  　交点Ｅ(ＢＥ',平行線(Ｅ",ＢＧ))、
  　交点Ｆ(Ｅ"Ｅ,平行線(Ｇ,ＢＥ))、
  　平四ＢＥＦＧ
  をとっている。

《ＡＢが
　ＢＥと一直線をなすように
　おかれ、》
ＦＧがＨまで延長され、
　Ａを通り
　ＢＧ、ＥＦのどちらかに平行に
　ＡＨがひかれ、 【・・・(b)】

• 命題１−３１（作図・平行線）
  による。
• 命題１−３０（平行の平行）
  により、
  　ＢＧ、ＥＦのどちらに平行にひいても、
  　他方とも平行になる。
• ＦＧ、ＢＧは
  　交わっているので、
  　命題１−３０の補足(交線に平行な線)
  により、
  　Ａを通りＢＧに平行な直線は
  　ＦＧと交わる。
  その交点をＨとする。
• 　交点Ｈ(延長ＦＧ,平行線(Ａ,ＢＧ)
  をとっている。

ＨＢが結ばれたとせよ。

• 公準１−１（作図.直線）
  による。
• 　線分ＨＢ
  をとっている。

そうすれば
　線分ＨＦが
　平行線ＡＨ、ＥＦと交わるから、
　角ＡＨＦ、ＨＦＥの和は２直角に等しい。

• (b) ,命題１−２９（平行と錯角、内対角、同側内角）
  による。
• 　∠ＡＨＦ＋∠ＨＦＥ＝２∠Ｒ
  となっている。

それゆえ
　角ＢＨＧ、ＧＦＥの和は
　２直角より小さい。

• ＢＨＧはＡＨＧの部分であるから、
  　公理１−８（大きい）
  により小さい。
• 　∠ＢＨＧ＋∠ＧＦＥ＜２∠Ｒ
  となっている。

そして
　その和が２直角より小さい２角から
　限りなく延長された
　２直線は交わる。

• 公準１−５（平行線公準）
  である。

ゆえに
　ＨＢ、ＦＥは
　延長されるとき、
　交わるであろう。

• 　前節、前々節による。
• 　ＨＢ╂ＦＥ
  となっている。

これらが
　延長されＫにおいて交わるとし、

• 　前節による。
• 　交点Ｋ(ＨＢ,ＦＥ)
  となっている。

　点Ｋを通り
　ＥＡ、ＦＨのどちらかに平行に
　ＫＬがひかれ、

• 命題１−３１（作図・平行線）
  による。
• 命題１−３０（平行の平行）
  により、
  　ＥＡ、ＦＨのどちらに平行にひいても、
  　他方とも平行になる。
• 　平行線ＫＬ'(Ｋ,ＥＡ)
  をとっている。

ＨＡ、ＧＢが
　Ｌ、Ｍまで延長されたとせよ。 【・・・(c)】

• 公準１−２（作図.直線の延長）
  による。
• 　交点Ｌ(延長ＨＡ,ＫＬ')、
  　交点Ｍ(延長ＧＢ,ＫＬ')
  をとっている。

そうすれば
　ＨＬＫＦは平行四辺形、

• 命題の設定 ,(a) (b) (c)
  定義の補足（命題１−３４）(平行四辺形・対角線)
  による。
• 　ＨＬＫＦ;平行四辺形
  となっている。

ＨＫは
　その対角線であり、
　ＡＧ、ＭＥは
　ＨＫをはさむ平行四辺形、
　ＬＢ、ＢＦは
　いわゆる補形である。
それゆえ
　ＬＢはＢＦに等しい。

• 命題１−４３（平行四辺形の補形）
  による。
• 　平四ＬＢ＝平四ＢＦ
  となっている。

ところが
　ＢＦは三角形Ｃに等しい。

• (a) による。
• 　平四ＢＦ＝△Ｃ
  となっている。

ゆえに
　ＬＢもＣに等しい。

• 公理１−１（同じものに等しい）
  による。
• 　平四ＬＢ＝△Ｃ
  となっている。

そして
　角ＧＢＥは角ＡＢＭに等しく、

• 命題１−１５（対頂角）
  による。
• 　∠ＧＢＥ＝∠ＡＢＭ
  となっている。

また
　ＧＢＥはＤに等しいから、
　角ＡＢＭも角Ｄに等しい。

• 公理１−１（同じものに等しい）
  による。
• 　∠ＡＢＭ＝∠Ｄ
  となっている。

よって
　与えられた線分ＡＢ上に
　与えられた三角形Ｃに等しい
　平行四辺形ＬＢが
　Ｄに等しい
　角ＡＢＭのなかにつくられた。
　
これが作図すべきことであった。

• この命題が、
  　直線図形を
  　指定された角におさまる
  　平行四辺形に
  　等積変形する第二歩である。
• 命題1-44は、
  　線分ＡＢ、
  　△Ｃ、
  　直線角Ｄ
  に対して、
  　半直線ＢＥ'(延長ＡＢ)、
  　線分ＢＧ'[;;∠Ｇ'ＢＥ'＝∠Ｄ,ＢＧ'＝辺1.△Ｃ]、
  　点Ｅ"(同側(ＢＧ',Ｅ'),△ＢＧ'Ｅ"≡△Ｃ)、
  　中点Ｇ(ＢＧ')、
  　交点Ｅ(ＢＥ',平行線(Ｅ",ＢＧ))、
  　交点Ｆ(Ｅ"Ｅ,平行線(Ｇ,ＢＥ))、
  　平四ＢＥＦＧ、
  　交点Ｈ(延長ＦＧ,平行線(Ａ,ＢＧ)、
  　交点Ｋ(ＨＢ,ＦＥ)、
  　平行線ＫＬ'(Ｋ,ＥＡ)、
  　交点Ｌ(延長ＨＡ,ＫＬ')、
  　交点Ｍ(延長ＧＢ,ＫＬ')
  をとれば、
  　平四ＬＢ＝△Ｃ
  　∠ＡＢＭ＝∠Ｄ
  のことである。
• 命題1-44は作図用命題である。

  前提	作図	推論
  定義		補（題1-34）
  公準	1-1、1-2、1-5
  公理		1-1、1-8
  命題	1-23、1-30補、 1-31、1-42	1-15、1-29、1-30、1-43
  その他		どちらかに

前 　　 次 　　 目次 　　頁頭