ユークリッド原論をどう読むか（１６）
頁末 　　 前 　　 次 　 目次

ユークリッド原論

第１１巻
　
命題１１ー９（同一直線に平行なら平行）
　　同一直線に平行であり、
　　それと［あわせて］同一平面上にない
　二つの直線は
　　互いにも平行である。

• 直線は、
  定義１ー４による。
• 平行は、
  定義１ー２３による。
• 平面は、
  定義１ー７による。

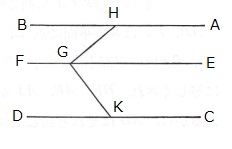
　ＡＢ、ＣＤの双方が
　　ＥＦに平行で、
　　それと同一平面上にない
とせよ。

• 　公準の補足２（命題１１ー２）(作図.空間に任意の平面をとる)
  により、
  　平面をとる。
  　公準１ー１の補足２（作図.任意の線分・直線をひく）
  により、
  　平面上に直線ＥＦをとる。
  　公準１ー１の補足（作図.任意の点をとる）
  により、
  　平面外に点をとる。
  　命題１１ー２の補足(作図.交わる２直線、１直線上にない３点、１直線とその上にない１点で平面が決定)
  により、
  　平面上の直線と平面外の点をとおる平面をとる。
  　命題１ー３１（作図・平行線）
  により、
  　それぞれの平面上に、
  　最初にとった直線に平行な直線ＡＢ、ＣＤをとる。
• 　ＡＢ‖ＥＦ、
  　ＣＤ‖ＥＦ、
  　ＣＤ；¬平面（ＡＢ、ＥＦ）上
  となっている。

　ＡＢは
　　ＣＤと平行である
と主張する。
　　　ＥＦ上に
　任意の点Ｇが
　　とられ、
　　　それから
　　　ＥＦ、ＡＢを通る平面上に
　　　ＥＦに直角に
　ＧＨが
　　ひかれ、
　　　ＦＥ、ＣＤを通る平面上に
　　　またＥＦに垂直に
　ＧＫが
　　ひかれた
とせよ。

• 　公準１ー１の補足（作図.任意の点をとる）、
  　命題１ー１１（作図・線分からの垂線）
  による。
• 　Ｇ（ＥＦ；）、
  　Ｈ（平面（ＥＦ、ＡＢ）；ＧＨ⊥ＥＦ）、
  　Ｋ（平面（ＥＦ、ＣＤ）；ＧＫ⊥ＥＦ）
  となっている。

そうすれば
　ＥＦは
　　ＧＨ、ＧＫの双方に垂直である

• 　前節
  による。
• 　ＥＦ⊥ＧＨ、ＧＫ
  となっている。

から、
　ＥＦは
　　　ＧＨ、ＧＫを通る平面に対しても
　　垂直である。

• 　命題１１ー４（交わる２直線に垂直な直線はそれらを通る平面にも垂直）
  による。
• 　ＥＦ⊥平面（ＧＨ、ＧＫ）
  となっている。

そして
　ＥＦは
　　ＡＢに平行である。

• 　命題の設定
  による。
• 　ＥＦ‖ＡＢ
  となっている。

それゆえ
　ＡＢも
　　ＨＧ、ＧＫを通る
　　平面に垂直である。

• 　前節、前々節、
  　命題１１ー８（平行線の一方が平面に垂直なら他方も垂直）
  による。
• 　ＡＢ⊥平面（ＨＧ、ＧＫ）
  となっている。

同じ理由で
　ＣＤも
　　ＨＧ、ＧＫを通る
　　平面に対し垂直である。

• 　前々節、前々々節、
  　命題１１ー８（平行線の一方が平面に垂直なら他方も垂直）
  による。
• 　ＣＤ⊥平面（ＨＧ、ＧＫ）
  となっている。

ゆえに
　ＡＢ、ＣＤの双方は
　　ＨＧ、ＧＫを通る
　　平面に対し垂直である。

• 　前節、前々節
  による。
• 　ＡＢ、ＣＤ⊥平面（ＨＧ、ＧＫ）
  となっている。

ところが
もし
　２直線が
　　同一平面に対し垂直である
ならば、
　それらの２直線は
　　平行である。

• 　命題１１ー６（同一平面に垂直な２直線は平行）
  による。

よって
　ＡＢは
　　ＣＤに平行である。

• 　前節、前々節
  による。
• 　ＡＢ‖ＣＤ
  となっている。

これが証明すべきことであった。

• 命題１１ー９は、
  　ＡＢ、ＣＤが
  　　ＥＦに平行で、
  　　それと同一平面上にない
  とすると、
  　ＥＦ上にとった点Ｇから、
  　　平面（ＥＦ、ＡＢ）上にＥＦの垂線ＧＨ、
  　　平面（ＥＦ、ＣＤ）上にＥＦの垂線ＧＫ
  をとると、
  　ＥＦ⊥平面（ＧＨ、ＧＫ）
  　ＡＢ、ＣＤ⊥平面（ＧＨ、ＧＫ）
  となり、
  　ＡＢ‖ＣＤ
  のことである。
• 命題１１ー９は推論用命題である。

  前提	作図・構成	推論
  定義
  公準	1-1補,1-1補2,補2(題11-2)
  公理
  命題	1-11,1-31,11-2補	11-4,11-6,11-8
  その他

前 　　 次 　　 目次 　　頁頭