ユークリッド原論をどう読むか（１６）
頁末 　　 前 　　 次 　 目次

ユークリッド原論

第１１巻
　
命題１１ー１（平面上の直線は平面外に出ない）
　直線のある［２点を含む］部分が
　　基準平面上に，
　ある部分が
　　その平面外に
　　　あることはできない。

• 　基準平面上にある部分が、
  　　単に１点だけ
  というのでは、
  　　原論の構成から考えて、
  　　　妥当でないので、
  　基準平面上にあるのは、
  　　２点を含む部分と修正しておく。
  これに対し、
  　基準平面外には１点だけでも
  　　出ていることはできないので、
  　　原文のままとする。
  
• 直線は、
  定義１ー４による。
• 平面は、
  定義１ー７による。

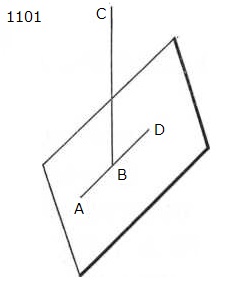
もし
可能ならば，
　線分ＡＢＣの《任意の》［２点を含む］部分ＡＢが
　　基準平面上
　　　にあり，

• 　公準１ー１の補足（作図.任意の点をとる）
  により、
  　２点Ａ、Ｂを基準平面上に
  とり、
  　公準１ー１（作図.直線）
  により
  　この２点を結ぶ直線
  をひく。
  　定義１ー７（平面）
  により、
  　この直線、
  　したがって、
  　線分ＡＢは、
  　　基準平面上にある。
  
• 　「もし可能ならば」は、
  　この後のことである。
  
• 　ＡＢ；基準平面上
  となっている。

　《任意の》［ある］部分Ｂ[']Ｃが
　　その平面外に
　　　あるとせよ。

• 　背理法の仮定である。
  　少なくとも点Ｃだけは、
  　　基準平面外にある
  と仮定するものとして、推論を進める。
  
• 　「任意の」という表現は
  　　適切でない。
  　コメント（命題５−８）を参照のこと。
  

そうすれば
　　基準平面上に
　　ＡＢと連続的に一直線をなす
　何らかの線分が
　　　あるであろう。

• 　定義１ー１５（円）
  により、
  　円は平面図形であり、
  　公準１ー３（作図.円）
  により、
  　中心Ｂ、半径ＢＡの円が、
  　基準平面上に描かれる。
  　公準１ー２（作図.直線の延長）
  により、
  　線分ＡＢがＢの方向に延長され、
  　命題３−１の補足２(中心を通る直線は円周と２交点)
  により、
  　延長された線分と円との交点をＢ1
  とすると、
  　ＡＢ1は、基準平面上の線分
  となる。
  　基準平面上の線分ＡＢ1について、
  同様に繰り返し、
  　基準平面上の線分ＡＢ2を描く。
  同様に繰り返すと、
  　公準１ー２の補足（アルキメデスの原理）
  により、
  　基準平面上の線分ＡＢを
  　　線分ＡＢＣより長くなるように、
  　　基準平面上に延長し、
  　　ＡＢＤとする。
  

　　それをＢＤ
とせよ。

• 　前節による。
• 　線分ＡＢ；基準平面上、
  　線分ＡＢＤ（延長ＡＢ；ＡＢＤ＞ＡＢＣ、基準平面上）
  となっている。

そうすれば
　ＡＢは
　　２線分ＡＢＣ,ＡＢＤの共通な部分
　　　である。
　これは
　　不可能
　　　である。

• 　命題１ー３の補足（作図.等しい線分となる点）
  により、
  　点Ｅ（ＢＤ；ＢＥ＝ＢＣ）
  をとると、
  　命題３−１の補足２(中心を通る直線は円周と２交点)
  により、
  　直線ＡＢにおいて、
  　ＢについてＡと反対側で、
  　Ｂからの距離がＢＣとなる点は１点であり、
  　異なる２点とはならない
  ことによる。
  

なぜなら
もし
　　Ｂを中心に
　　ＡＢを半径として
　　円を
　　　描け
ば，
　二つの直径は
　　円の不等な弧を
　　　切りとるであろう
から。

• 　「なぜならもし」は、
  　コメント（命題１ー４）参照のこと。
  
• 　本文は
  　　ＡＢ≦ＢＣ
  と仮定して推論している。
  　Ｆ（ＡＢ；ＦＢ＝ＢＣ）
  をとることは可能だから、
  　Ｆを改めてＡとして、
  　ＡＢ≦ＢＣ
  とすることは一般性を失わない。
  　「２つの直径」とは、
  　半径ＡＢとなる距離を
  　　ＢからＡと反対側に取ったとき、
  　　基準平面上にない点がとれるという背理法の仮定と、
  　　基準平面上にとれるという推論の結果
  により
  　直径が２つとれることを踏まえている。
  　「円の不等な弧を切りとる」とは、
  　　１つの半径を延長して、
  　　２つの異なる直径となる
  ことにより、
  　元の半径のＡからＢを見るときの一方の側に
  　２つの異なる半円ができる
  ことになって
  矛盾が生じていることを述べている。
  しかし、
  この矛盾が顕在化する前に、
  　１つの半径を延長して、
  　２つの異なる直径となる
  ことが矛盾である。
  推論が混乱している。
  と言わざるをえない。
  
• 　「なぜならもし」は、
  　コメント（命題１ー４）参照のこと。
  これと、
  　コメント（命題５−８）を踏まえると、
  　後世の不適切なコメントの混入が
  　　疑われる。
  

よって
　直線のある部分が
　　基準平面上に，
　ある部分が
　　その平面外に
　　　あることはできない。

• 　前節、
  　背理法による。

これが証明すべきことであった。

• 　原論の論証を尊重すれば、
  　定義１ー１５（円）
  において、
  　円が平面図形である
  と明記していることが
  　本命題の証明の根拠になっている。
  しかし、
  　定義１ー７（平面）
  によれば、
  　「平面とは
  　その上にある直線について
  　一様に横たわる面である。」
  これにより、
  　本命題を論証をすることができる。
  すなわち、
  　直線の一部の線分が基準平面上に横たわっている。
  　定義１ー７（平面）
  により、
  　平面とは
  　その上にある直線について
  　一様に横たわる面である。
  よって、
  　直線は基準平面上に横たわっており、
  　一部が基準平面上から出ることはない。
  なお、
  　原論第一巻の定義において、
  　平面上であることを明記しているのは、
  　定義１ー１５（円）と、
  　定義１ー２３（平行(線)）
  だけである。
  
• 命題１１ー１は、
  　直線ＡＢＣの一部の線分ＡＢが
  　　基準平面上にあれば、
  　全体ＡＢＣが
  　　基準平面上にある
  ことである。
  
• 命題１１ー１は推論用命題である。

  前提	作図・構成	推論
  定義		1-7,1-15
  公準	1-1,1-1補,1-2,1-2補,1-3
  公理
  命題	1-3補	3-1補2
  その他		コ(題1-4),コ(題5-8)

前 　　 次 　　 目次 　　頁頭