ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第１０巻
　
命題１０ー３３補助（直角三角形の垂線の足による矩形と辺上の正方形）

補　助　定　理

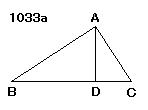
　ＡＢＣを
　直角Ａをもつ直角三角形
とし、
　垂線ＡＤがひかれた
とせよ。
　矩形ＣＢ、ＢＤはＢＡ上の正方形に等しく、
　矩形ＢＣ、ＣＤはＣＡ上の正方形に等しく、
　矩形ＢＤ、ＤＣはＡＤ上の正方形に等しく、
さらに
　矩形ＢＣ、ＡＤは矩形ＢＡ、ＡＣに等しい
と主張する。

• 直角は、
  定義１ー１０による。
• 直角三角形は、
  定義１ー２１による。
• 垂線は、
  定義１ー１０による。
• 矩形は、
  定義１ー２２による。
• 正方形は、
  定義１ー２２による。
• 等しいは、
  公理１ー７による。

• 　命題を一般的に言葉で表現する
  ことを省いて、いきなり、
  　具体的に図形を文字でしている。
  　これは、
  　補助定理
  においても、
  　異例である。
  

そしてまず
　矩形ＣＢ、ＢＤがＢＡ上の正方形に等しいこと。

• 　第一に証明する命題
  であることを明示している。
  

　直角三角形において
　直角から底辺に垂線ＡＤがひかれた

• 　命題１ー１２（作図・線分への垂線）　
  による。
  
• 　ＡＤ⊥ＢＣ
  となっている。
  

から、
　三角形ＡＢＤ、ＡＤＣはＡＢＣ全体に対し、
また
　相互に相似である。
　　　　　　[......(１)]

• 　前節、
  　命題６ー８（直角三角形の垂線と相似）
  による。
• 　△ＡＢＤ∽△ＡＢＣ、
  　△ＡＤＣ∽△ＡＢＣ、
  　△ＡＢＤ∽△ＡＤＣ
  となっている。
  

そして
　三角形ＡＢＣは三角形ＡＢＤに相似である

• 　前節による。
• 　△ＡＢＣ∽△ＡＢＤ、
  となっている。

から、
　ＣＢがＢＡに対するように、
　ＢＡがＢＤに対する。

• 　前節、
  　定義６ー１（相似）
  による。
• 　ＣＢ：ＢＡ＝ＢＡ：ＢＤ
  となっている。
  

したがって
　矩形ＣＢ、ＢＤはＡＢ上の正方形に等しい。

• 　前節、
  　命題６ー１７（比例３線分と外項矩形、中項正方形）
  による。
• 　rec(ＣＢ、ＢＤ)＝sq(_ＡＢ)
  となっている。
  

同じ理由で
　矩形ＢＣ、ＣＤもＡＣ上の正方形に等しい。

• 　△ＡＢＣ∽△ＡＤＣ、
  より、
  　ＢＣ：ＣＡ＝ＡＣ：ＣＤ
  よって、
  　rec(ＢＣ、ＣＤ)＝sq(_ＡＣ)
  となっている。
  

そしてもし
　直角三角形において
　直角から底辺へ垂線がひかれる
ならば、

• 　この「もし」は、
  　条件（仮定条件）を示している。
  　背理法の条件ではない。
  

　ひかれた垂線は
　底辺の二つの部分の比例中項である

• 　命題６ー８の系（直角三角形の垂線は比例中項）
  のことである。
  

から、
　ＢＤがＤＡに対するように、
　ＡＤがＤＣに対する。　

• 　前節、
  　定義の補足３（命題６ー８）(比例中項)
  による。
  
• 　ＢＤ：ＤＡ＝ＡＤ：ＤＣ
  となっている。

したがって
　矩形ＢＤ、ＤＣはＤＡ上の正方形に等しい。

• 　前節、
  　命題６ー１７（比例３線分と外項矩形、中項正方形）
  による。
  
• 　rec(ＢＤ、ＤＣ)＝sq(_ＤＡ)
  となっている。
  

　矩形ＢＣ、ＡＤも矩形ＢＡ、ＡＣに等しい
と主張する。

先に述べたように
　ＡＢＣはＡＢＤに相似である

• 　（１）による。
• 　△ＡＢＣ∽△ＡＢＤ
  となっている。
  

から、
　ＢＣがＣＡに対するように、
　ＢＡがＡＤに対する。

• 　前節、
  　定義６ー１（相似）
  による。
  
• 　ＢＣ：ＣＡ＝ＢＡ：ＡＤ
  となっている。
  

したがって
　矩形ＢＣ、ＡＤは矩形ＢＡ、ＡＣに等しい。

• 　前節、
  　命題６ー１６（比例４線分と外項矩形、内項矩形）
  による。
  
• 　rec(ＢＣ、ＡＤ)＝rec(ＢＡ：ＡＣ) となっている。

これが証明すべきことであった。

• 命題１０ー３３補助は、
  　△ＡＢＣ；直角三角形（∠Ａ；直角）
  において、
  　Ｄ；ＢＣ上で、ＡＤ⊥ＢＣ
  ならば、
  　rec(ＣＢ、ＢＤ)＝sq(_ＡＢ)、
  　rec(ＢＣ、ＣＤ)＝sq(_ＣＡ)、
  　rec(ＢＤ、ＤＣ)＝sq(_ＤＡ)、
  　rec(ＢＣ、ＡＤ)＝rec(ＢＡ、ＡＣ)
  のことである。
  
• 命題１０ー３３補助は推論用命題である。

  前提	作図・構成	推論
  定義		6-1,補3(題6-8)
  公準
  公理
  命題	1-12	6-8,6-8系,6-16,6-17
  その他

前 　　 次 　　 目次 　　頁頭