ユークリッド原論をどう読むか（１３）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第９巻
　
命題９ー３５（順次比例の２項ー初項：末項ー初項）
もし
　任意個の数が順次に比例し、
　第２項と末項から
　それぞれ初項に等しい数が引き去られる
ならば、
　第２項と初項との差が
　初項に対するように、
　末項と初項との差が
　末項より前のすべての項の和に対する
であろう。

• 数は、
  定義７ー２による。
• 順次に比例は、
  定義の補足（命題８ー１）による。
• 項は、
  定義５ー８の補足による。
• 初項・末項は、
  定義の補足（命題８ー７）による。
• 等しいは、
  公理１ー７による。
• 対する・ようには、
  定義の補足３（命題５ー１１）による。

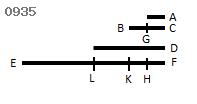
　最小である数Ａから始まり、
　順次に比例する任意個の数
　Ａ、ＢＣ、Ｄ、ＥＦがある
とし、
　ＢＣ、ＥＦから
　Ａに等しいＢＧ、ＦＨが
　それぞれ引き去られた
とせよ。

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
  
• 　準一般的な証明である。
  　コメント２（命題５ー１）
  　参照のこと。
  
• 　Ａ、ＢＣ、Ｄ、ＥＦ（順次に比例）
  　ＢＧ＝Ａ、ＦＨ＝Ａ、
  　ＢＣーＢＧ＝ＧＣ、
  　ＥＦーＦＨ＝ＥＨ
  となっている。
  

　ＧＣがＡに対するように、
　ＥＨがＡ、ＢＣ、Ｄの和に対する
と主張する。

　ＦＫをＢＣに等しく、
　ＦＬをＤに等しく
せよ。
　　　　　　[......(ａ)]

• 　ＦＫ＝ＢＣ、
  　ＦＬ＝Ｄ
  となっている。

そうすれば
　ＦＫはＢＣに等しく、
そのうち
　ＦＨはＢＧに等しい

• 　前節、 命題の設定による。
• 　ＦＫ＝ＢＣ。
  　ＦＨ＝ＢＧ
  となっている。

から、
　残りのＨＫは残りのＧＣに等しい。
　　　　　　[......(１)]

• 　前節、
  　公理１ー３（等しいものから等しいものをひく）
  による。
  
• 　ＨＫ＝ＧＣ
  となっている。

そして
　ＥＦがＤに対するように、
　ＤがＢＣに、
　ＢＣがＡに対し、

• 　命題の設定による。

　ＤはＦＬに、
　ＢＣはＦＫに、
　ＡはＦＨに等しい

• 　（ａ）、 命題の設定による。

から、
　ＥＦがＦＬに対するように、
　ＬＦがＦＫに、
　ＦＫがＦＨに対する。

• 　前節、
  　命題５ー１１の補足２（等しい量は同じ比をもつ）
  による。
  

　分割比により
　ＥＬがＬＦに対するように、
　ＬＫがＦＫに、
　ＫＨがＦＨに対する。
定義５ー１５（比の分割・分割比）

• 　前節、
  　命題７ー１１（残りも全体と比例）
  による。
  

それゆえ
　前項の一つが
　後項の一つに対するように、
　前項の総和が
　後項の総和に対する。

• 　命題７ー１２（比例する前項・後項の総和）
  のことである
  

ゆえに
　ＫＨがＦＨに対するように、
　ＥＬ、ＬＫ、ＫＨの和が
　ＬＦ、ＦＫ、ＨＦの和に対する。

• 　前節、前々節による。
• 　ＫＨ：ＦＨ
  　＝ＥＬ＋ＬＫ＋ＫＨ：ＬＦ＋ＦＫ＋ＨＦ
  となっている。
  

ところが
　ＫＨはＣＧに、
　ＦＨはＡに、
　ＬＦ、ＦＫ、ＨＦの和は
　Ｄ、ＢＣ、Ａの和に等しい。

• 　（１）、 命題の設定、 （ａ）による。
• 　ＫＨ＝ＣＧ、ＦＨ＝Ａ、
  　ＬＦ＋ＦＫ＋ＨＦ＝Ｄ＋ＢＣ＋Ａ
  となっている。
  

したがって
　ＣＧがＡに対するように、
　ＥＨがＤ、ＢＣ、Ａの和に対する。

• 　前節、前々節、
  　命題５ー１１の補足２（等しい量は同じ比をもつ）
  による。
  

それゆえ
　第２項と初項との差が
　初項に対するように、
　末項と初項との差が
　末項より前のすべての項の和に対する。
　これが証明すべきことであった。

• 命題９ー３５は、
  　Ａ1、Ａ2、…、Ａn、Ａn+1；順次比例
  ならば、
  　(Ａ2−Ａ1)：Ａ1
  　＝(Ａn+1−Ａ１)：(Ａ1＋Ａ2＋…＋Ａn)
  のことである。
• 命題９ー３５は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理		1-3
  命題		5-11補2,7-11,7-12
  その他	コ4(題7-1)	コ2(題5-1)

前 　　 次 　　 目次 　　頁頭