ユークリッド原論をどう読むか（１２）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第８巻
　
命題８ー２６（相似な平面数の比は平方数の比）
　相似な平面数は
　互いに
　平方数が平方数に対する比をもつ。

• 相似は、
  定義７ー２２による。
• 平面数は、
  定義７ー１７による。
• 平方数は、
  定義７ー１９による。
• 対するは、
  定義の補足３（命題５ー１１）による。
• 比は、
  定義５ー３による。

　Ａ、Ｂを相似な平面数
とせよ。

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
  
• 　数Ｇ、Ｈ、Ｋ、Ｌがあって、
  　Ａ＝Ｇ×Ｈ、Ｂ＝Ｋ×Ｌ、
  　Ｇ：Ｈ＝Ｋ：Ｌ
  となっている。
  

　ＡはＢに対し、
　平方数が平方数に対する比をもつ
と主張する。

　Ａ、Ｂは相似な平面数である

• 　命題の設定による。

から、
　Ａ、Ｂの間には
　１つの比例中項数が入る。

• 　前節、
  　命題８ー１８（相似な平面数と比例中項）
  による。
  

　入る
とし、
　それをＣ
とし、

• 　前節、前々節、
  　命題８ー１８の補足（構成.相似な平面数の比例中項）
  により、
  　Ｇ×Ｌ＝Ｃ
  となっている。
  

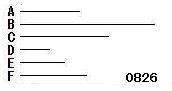
　Ａ、Ｃ、Ｂと同じ比をもつ数のうちで
　最小の数Ｄ、Ｅ、Ｆがとられた
とせよ。
　　　　　　[......(ａ)]

• 　命題８ー２（構成.順次に比例する最小の数）
  による。
  
• 　Ａ：Ｃ：Ｂ＝Ｄ：Ｅ：Ｆ（最小）
  となっている。
  

そうすれば
　それらの外項Ｄ、Ｆは
　平方数である。

• 　Ａ：Ｃ＝Ｍ：Ｎ（最小）
  とすると、
  　命題８ー２（構成.順次に比例する最小の数）
  により、
  　Ｄ＝Ｍ^2、Ｅ＝Ｍ×Ｎ、Ｆ＝Ｎ^2
  となっている。　
  

そして
　ＤがＦに対するように、
　ＡがＢに対し、

• 　（ａ）による。
• 　Ｍ^2：Ｎ^2＝Ａ：Ｂ となっている。

　Ｄ、Ｆは平方数である
から、
　ＡはＢに対し、
　平方数が平方数に対する比をもつ。

• 　前節。前々節による。

　これが証明すべきことであった。

• 　Ａ、Ｂが相似な平面数
  ならば、
  　Ａ：Ｂ＝Ｄ^2:Ｆ^2
  
• 命題８ー２６は推論用命題である。

  前提	作図	推論
  定義
  公準
  公理
  命題	8-2, 8-18補	8-18
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭