ユークリッド原論をどう読むか(11)
頁末
前
次
目次
ユークリッド原論
第7巻
命題7ー39(構成.数個の等分をもつ最小数)
「等分の作図は」
与えられた数個の
《約数》[等分]をもつ
最小の数を見いだす
こと。
-
等分は、
定義の補足(命題7ー37)による。
中村幸四郎他訳では、
約数となっているが、
約数とすれば、
命題7ー36(3数の最小公倍数)
と実質的に同じであり、
命題として取り上げる意味がない。
等分された1つ分という
a part の意味として、
等分とする方が妥当である。
Euclid's Elements
(Clark University Professor D.E.Joyceの
http://aleph0.clarku.edu/~djoyce/java/elements/elements.html)
においては、
Suppose
you want to find
the smallest number
with given parts,
say,
a fourth part and sixth part.
Then
take the LCM(4,6) which is 12.
The number 12 has
a 1/4 part,namely 3,
and a 1/6,namely 2.
とコメントしている。
- 最小は、
定義の補足3(命題3ー7)による。
- 数は、
定義7ー2
による。
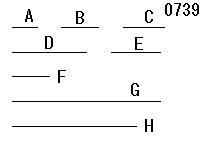
与えられた
《約数》[等分]を
A、B、C
とせよ。
-
等分は、
元来、
等分される数Zを定めて後に、
Zとの関係として定義される。
A、B、C
が直接作図されるものではない
(以下、コメント2(命題7ー39))
(等分の作図)という。
-
準一般的な証明である。
コメント2(命題5ー1)
を参照のこと。
-
等分A、B、C、
を仮想している。
作図されてはいない。
このとき
《約数》[等分]
A、B、Cをもつ
最小の数を見いださ
ねばならぬ。
D、E、Fを
《約数》[等分]A、B、Cと
同名の数
とし、
[......(a)]
-
定義の補足(命題7ー38)(同名の数)
による。
-
同名数D(等分A)、
同名数E(等分B)、
同名数F(等分C)
をとっている。
D、E、Fは作図される。
D、E、Fに割り切られる
最小の数Gがとられた
とせよ。
[......(b)]
-
命題7ー36(3数の最小公倍数)
による。
-
最小公倍数G(D,E,F)
をとっている。
そうすれば
Gは
D、E、Fと
同名の《約数》[等分]をもつ。
-
命題7ー37(割り切れるなら同名の等分数が存在)
による。
-
((同名等分(D)、同名等分(E)、同名等分(F)).G);存在
となっている。
ところが
A、B、Cは
D、E、Fと
同名の《約数》[等分]である。
-
(a)
による。
-
(等分A、等分B、等分C);=(同名等分(D),同名等分(E),同名等分(F))
となっている。
ゆえに
Gは
《約数》[等分]
A、B、Cをもつ。
-
前節、前々節による。
-
(等分A、等分B、等分C).G;存在
となっている。
次に
最小でもある
と主張する。
もし
最小でない
ならば、
《約数》[等分]
A、B、Cをもつ
Gより小さい何らかの数がある
であろう。
それをH
とせよ。
-
背理法の仮定である。
-
数H[;;((等分A、B、C).H);存在,<G)
をとっている。
Hは
《約数》[等分]
A、B、Cをもつ
から、
Hは
《約数》[等分]
A、B、Cと同名の数に
割り切られる
であろう。
-
命題7ー38(等分(数)と同名の数で割り切る)
による。
-
同名数(等分A、等分B、等分C)|H
となっている。
ところが
D、E、Fは
《約数》[等分]
A、B、Cと同名の数である。
-
(a)による。
-
(D、E、F);同名数(等分A、等分B、等分C)
となっている。
したがって
Hは
D、E、Fに割り切られる。
-
前節、前々節による。
-
(D、E、F)|H
となっている。
そして
Gより小さい。
-
背理法の仮定による。
-
G;最小公倍数(D,E,F)、
H;(D、E、F)|H、<G
となっている。
これは不可能である。
よって
Hより小さくて
《約数》[等分]
A、B、Cをもつ
いかなる数もない
であろう。
これが証明すべきことであった。
-
等分(単位分数)が独立して登場する
最初の命題である。
- 命題7ー39は、
等分A、B、C
に対して、
最小公倍数G(同名数(A、B、C))
をとれば、
G;((等分(A、B、C).G);存在)、最小
のことである。
- 命題7ー39は構成用命題である。
前
次
目次
頁頭
