ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー２８（互いに素の和・差は対して素）
もし
　２つの数が
　互いに素である
ならば、
　それらの和も
　２数の双方に対して素であろう。

そして
もし
　２数の和が
　それらの１つに対し素である
ならば、
　最初の２数も互いに素であろう。

• 数は、 定義７ー２による。
• 互いに素は、 定義７ー１３による。
• 対して素は、 定義の補足（命題７ー２３）による。

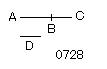
　互いに素である２数ＡＢ、ＢＣが
　加えられた
とせよ。

• 「数（について）・・・とせよ」は、 コメント４（命題７ー１）参照のこと。

　和ＡＣは
　ＡＢ、ＢＣの双方に対し素である
と主張する。

もし
　ＣＡ、ＡＢが
　互いに素でない
ならば、

• 背理法の仮定を述べようとしている。

　何らかの数が
　ＣＡ、ＡＢを割り切るであろう。

　割り切る
とし、
　それをＤ
とせよ。

• 背理法の仮定である。
  Ｄ｜ＣＡ、Ｄ｜ＡＢとなっている。

そうすれば
　Ｄは
　ＣＡ、ＡＢを割り切る
から、
　残りのＢＣをも割り切るであろう。

• 命題７ー１の補足２（倍数の和・差は倍数） による。

ところが
　ＢＡをも割り切る。

• 背理法の仮定による。

それゆえ
　Ｄは
　互いに素であるＡＢ、ＢＣを割り切る
ことになる。

• 前節、前々節の結果による。

　これは不可能である。

• 命題の設定（互いに素）に矛盾する。

ゆえに
　いかなる数も
　数ＣＡ、ＡＢを割り切らない
であろう。

• 背理法による。

したがって
　ＣＡ、ＡＢは互いに素である。

　同じ理由
で
　ＡＣ、ＣＢも互いに素である。

よって
　ＣＡはＡＢ、ＢＣの双方に対し素である。

また
　ＣＡ、ＡＢが互いに素である
とせよ。

　ＡＢ、ＢＣも互いに素である
と主張する。

もし
　ＡＢ、ＢＣが
　互いに素でない
ならば、

• 背理法の仮定を述べようとしている。

　何らかの数が
　ＡＢ、ＢＣを割り切るであろう。

　割り切る
とし、
　それをＤ
とせよ。

• 背理法の仮定である。

そうすれば
　Ｄは
　ＡＢ、ＢＣの双方を割り切る
から、
　ＣＡ全体をも割り切るであろう。

• 命題７ー１の補足２（倍数の和・差は倍数） による。

ところが
　ＡＢをも割り切る。

• 背理法の仮定による。

それゆえ
　Ｄは
　互いに素であるＣＡ、ＡＢを割り切る
ことになる。

• 前節、前々節の結果である。

　これは不可能である。

• 命題の設定（互いに素）に矛盾する。

ゆえに
　いかなる数も
　ＡＢ、ＢＣを割り切らないであろう。

• 背理法による。

よって
　ＡＢ、ＢＣは互いに素である。

• 定義７ー１３（互いに素） による。

　これが証明すべきことであった。

• 命題７ー２８は推論用命題である。

  前提	作図	推論
  定義		7-13
  公準
  公理
  命題		7-1補2
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭