ユークリッド原論をどう読むか（９517）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第５巻

命題５ー１７（比例ならば分割比も比例）
もし
　量が
　合比によって［得られた］比例する［量］
ならば、
　分割比によっても
　比例するであろう。

• 量は、定義５ー１の補足 による。
• 合比は、定義５ー１４ による。
• 比例は、定義５ー６ による。
• 分割比は、定義５ー１５ による。

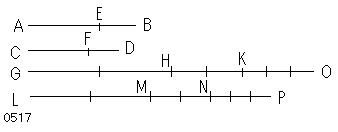
ＡＢ、ＢＥ、ＣＤ、ＤＦを
　合比によって［得られた］比例する量とし、
　ＡＢがＢＥに対するように、
　ＣＤがＤＦに対するとせよ。

• 同じ比をもつ線分の作図（仮想的）は、
  　コメント２（命題５ー４）参照のこと
• 　ＡＢ、ＢＥ、ＤＦ
  に対して、
  　ＣＤ(;;ＡＢ：ＢＥ＝ＣＤ：ＤＦ)
  をとっている。

それらは分割比によっても比例し、
　ＡＥがＥＢに対するように
　ＣＦがＤＦに対するであろう
　と主張する。
　
ＡＥ、ＥＢ、ＣＦ、ＦＤの［任意の］同数倍
　ＧＨ、ＨＫ、ＬＭ、ＭＮと
　ＥＢ、ＦＤの別の任意の同数倍
　ＫＯ、ＮＰとが
　とられたとせよ。【・・・(a)】

• 推論の設定である。
• 量の倍は、命題の補足（定義５ー２）（作図.倍量）
  による。
• ＫＯ、ＮＰについては、
  　別の同数倍を作図しておいて、
  　それぞれＧＫ、ＬＮに対して
  　量の和（命題の補足（定義５ー１４）（作図.量の和））をおこなっている。
  
• ［任意の］同数倍は、コメント（命題５ー４）参照のこと。
• 　(ＧＨ、ＨＫ、ＬＭ、ＭＮ)＝ｍ(ＡＥ、ＥＢ、ＣＦ、ＦＤ)、
  　(ＫＯ、ＮＰ)＝ｎ(ＥＢ、ＦＤ)
  をとっている。

そうすれば
　ＧＨはＡＥの、
　ＨＫはＥＢの同数倍であるから、

• (a) による。
• 　倍数(ＧＨ,ＡＥ)＝倍数(ＨＫ,ＥＢ)＝ｍ
  となっている。

　ＧＨはＡＥの、
　ＧＫはＡＢの同数倍である。【・・・(1)】

• 命題５ー１（同数倍の和１）
  による。
• 　倍数(ＧＨ,ＡＥ)＝倍数(ＧＫ,ＡＢ)＝ｍ
  となっている。

ところが
　ＧＨはＡＥの、
　ＬＭはＣＦの同数倍である。【・・・(2)】

• (a) による。
• 　倍数(ＧＨ,ＡＥ)＝倍数(ＬＭ,ＣＦ)＝ｍ
  となっている。

それゆえ
　ＧＫはＡＢの、
　ＬＭはＣＦの同数倍である。【・・・(3)】

• (1) (2) による。
• 　倍数(ＧＫ,ＡＢ)＝倍数(ＬＭ,ＣＦ)＝ｍ
  となっている。

また、
　ＬＭはＣＦの、
　ＭＮはＦＤの同数倍であるから、

• (a) による。
• 　倍数(ＬＭ,ＣＦ)＝倍数(ＭＮ,ＦＤ)＝ｍ
  となっている。

　ＬＭはＣＦの、
　ＬＮはＣＤの同数倍である。【・・・(4)】

• 命題５ー１（同数倍の和１）
  による。
• 　倍数(ＬＭ,ＣＦ)＝倍数(ＬＮ,ＣＤ)＝ｍ
  となっている。

ところが
　ＬＭはＣＦの、
　ＧＫはＡＢの同数倍であった。

• (3) による。
• 　倍数(ＬＭ,ＣＦ)＝倍数(ＧＫ,ＡＢ)＝ｍ
  となっている。

ゆえに
　ＧＫはＡＢの、
　ＬＮはＣＤの同数倍である。

• (4) による。
• 　倍数(ＧＫ,ＡＢ)＝倍数(ＬＮ,ＣＤ)＝ｍ
  となっている。

したがって
　ＧＫ、ＬＮはＡＢ、ＣＤの同数倍である。【・・・(5)】

• 　ＧＫ＝ｍＡＢ、
  　ＬＮ＝ｍＣＤ
  となっている。

また
　ＨＫはＥＢの、
　ＭＮはＦＤの同数倍であり、
　ＫＯはＥＢの、
　ＮＰはＦＤの同数倍であるから、

• (a) による。
• 　(ＨＫ、ＭＮ)＝ｍ(ＥＢ、ＦＤ)、
  　(ＫＯ、ＮＰ)＝ｎ(ＥＢ、ＦＤ)
  となっている。

　和ＨＯはＥＢの、
　［和］ＭＰはＦＤの同数倍である。【・・・(6)】

• 命題５ー２（同数倍の和２）
  による。
• 　ＨＯ(;＝ＨＫ＋ＫＯ)＝(ｍ＋ｎ)ＥＢ、
  　ＭＰ(;＝ＭＮ＋ＮＰ)＝(ｍ＋ｎ)ＦＤ
  となっている。

そして
　ＡＢがＢＥに対するように、
　ＣＤがＤＦに対し、

• 命題の設定 による。
• 　ＡＢ：ＢＥ＝ＣＤ：ＤＦ
  となっている。

　ＡＢ、ＣＤの同数倍ＧＫ、ＬＮと
　ＥＢ、ＦＤの同数倍ＨＯ、ＭＰとがとられたから、

• (5) (6) による。
• 　(ＧＫ、ＬＮ)＝ｍ(ＡＢ、ＣＤ)、
  　(ＨＯ、ＭＰ)＝(ｍ＋ｎ)(ＥＢ、ＦＤ)
  となっている。

　もし
　ＧＫがＨＯより大きければ
　ＬＮもＭＰより大きく、
　等しければ、等しく、
　小さければ、小さい。
【・・・(7)】

• 　前項、前々項、
  　定義５ー５（同じ比）
  による。
• 　ＧＫ(＜、＝、＞)ＨＯ、
  ならば、
  　ＬＮ(＜、＝、＞)ＭＰ
  となっている。

ＧＫがＨＯより大きいとし、【・・・(b)】

• 推論の設定である。
• 　ＧＫ＞ＨＯ
  としている。

　双方からＨＫがひかれれば、
　ＧＨはＫＯより大きい。

• 公理１ー４の補足２（不等なものから等しいものをひく）
  による。
• 　ＧＨ＞ＫＯ
  となっている。

ところがもし
　ＧＫがＨＯより大きかったならば、
　ＬＮもＭＰより大きかった。

• (7) による。
• 　ＧＫ＞ＨＯ
  ならば、
  　ＬＮ＞ＭＰ
  となっていた。

それゆえ
　ＬＮはＭＰより大きく、
　双方からＭＮがひかれれば、
　ＬＭもＮＰより大きい。【・・・(8)】

• 公理１ー４の補足２（不等なものから等しいものをひく）
  による。
• 　ＬＮ＞ＭＰ、
  　ＬＭ＞ＮＰ
  となっている。

ゆえにもし
　ＧＨがＫＯより大きいならば、
　ＬＭもＮＰより大きい。

• (b) (8) による。
• 　ＧＨ＞ＫＯ
  ならば、
  　ＬＭ＞ＮＰ
  となっている。

同様にしてもし
　ＧＨがＫＯに等しければ、
　ＬＭもＮＰに等しく、
　小さければ、小さいことを証明しうる。

• 　ＧＫ(＝、＜)ＫＯ
  ならば、
  　ＬＭ(＝、＜)ＮＰ
  となっている。

そして
　ＧＨ、ＬＭはＡＥ、ＣＦの［任意］の同数倍であり、
　ＫＯ、ＮＰはＥＢ、ＦＤの別の任意の同数倍である。

• (a) による。
• ［任意の］同数倍は、コメント（命題５ー４）参照のこと。
• 　(ＧＨ、ＬＭ)＝ｍ(ＡＥ、ＣＦ)、
  　(ＫＯ、ＮＰ)＝ｎ(ＥＢ、ＦＤ)
  となっている。

したがって
　ＡＥがＥＢに対するように、
　ＣＦがＦＤに対する。

• 定義５ー５（同じ比）
  による。
• 　ＡＥ：ＥＢ＝ＣＦ：ＦＤ
  となっている。

　
よってもし
　量が
　合比によって［得られた］比例する［量］
ならば、
　分割比によっても
　比例するであろう。
これが証明すべきことであった。

• 　Ａ、Ｂ、Ｃ、Ｄを
  　合比によって得られた比例する量とする
  のは、
  　Ａ＝Ｂの場合を除くため
  である。
• 　Ａ、Ｂが任意の位置にあっても、
  　命題１ー３（作図・等しい線分を切り取る）
  により、
  　Ｂに等しいＢ'を
  　Ａの一端にとることができる
  ので
  　本命題が成立する。
  
• 命題５ー１７は、
  　Ａ：Ｂ＝Ｃ：Ｄ、
  　Ａ≠Ｂ
  ならば、
  　（ＡーＢ）：Ｂ＝（ＣーＤ）：Ｄ
  のことである。
• 命題５ー１７は推論用命題である。

  前提	作図	推論
  定義		5-5
  公準
  公理		1-4補2
  命題	補(義5-2),補(義5-14)	5-1,5-2
  その他		コ(題5-4),コ2(題5-4)

前 　　 次 　　 目次 　　頁頭