ユークリッド原論をどう読むか（４）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー３７（三角形の等積変形１）
同じ底辺の上にあり
　かつ
　同じ平行線の間にある三角形は
　互いに等しい。

• 底辺は、定義の補足（命題１ー３５）による。
• 平行線は、定義１ー２３による。
• 三角形は、定義１ー１９の補足２による。
• 等しいは、公理１ー７による。
  　三角形についての「等しい」が
  　ここで初めて
  　明確に面積のことであることがわかる。

ＡＢＣ、ＤＢＣを
　同じ底辺ＢＣの上にあり
　かつ
　同じ平行線ＡＤ、ＢＣの間にある
　三角形とせよ。

• 　線分ＢＣ
  に対して、
  　点Ａ[外.ＢＣ]、
  　平行線ＡＤ(Ａ,ＢＣ)、
  　三角形ＡＢＣ、ＤＢＣ、
  をとっている。

　三角形ＡＢＣは
　三角形ＢＤＣに等しいと主張する。


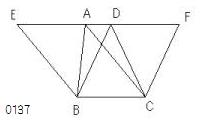
ＡＤが
　両方向にＥ、Ｆまで延長され、

• 公準１ー２（作図.直線の延長）
  による。
• Ａについて
  　Ｄと反対側にＥがあり、
  　Ｄについて
  　Ａと反対側にＦがある
  　ようにしている。
  
  • 　反対側は、定義１ー４の補足２（同じ側・反対側(直線)）
    による
  • 　ＡＥとＤＦが重ならない、
    　この場合については、
    　命題１ー３５（平行四辺形の等積変形１）
    で原論が証明している場合である。
    　

Ｂを通りＣＡに平行に
　ＢＥがひかれ、

• 命題１ー３１（作図・平行線）
  により平行線がひかれ、
  　命題１ー３０の補足(交線に平行な線)
  により
  　この平行線とＡＤの延長が交わる。
  この交点を溯ってＥとしている。
• 　交点Ｅ(ＤＡ,平行線(Ｂ,ＣＡ))、
  　線分ＢＥ
  をとっている。

Ｃを通りＢＤに平行に
　ＣＦがひかれたとせよ。
　　　　　　【・・・(1)】

• 　命題１ー３１（作図・平行線）、
  　命題１ー３０の補足(交線に平行な線)
  による。
• 　交点Ｆ(ＡＤ,平行線(Ｃ,ＢＤ))、
  　線分ＣＦ
  をとっている。

そうすれば
　ＥＢＣＡ、ＤＢＣＦの双方は
　平行四辺形である。

• 　(1),
  　定義の補足（命題１ー３４）(平行四辺形・対角線)
  による。
  
• 　ＥＢＣＡ、ＤＢＣＦ;平行四辺形
  となっている。

しかも等しい。
　　　　　　【・・・(2)】
なぜなら
　同じ底辺ＢＣの上にあり
　かつ
　同じ平行線とＢＣ、ＥＦの間にあるから。

• 「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。
• 命題１ー３６（平行四辺形の等積変形２）
  による。
• 　平四ＥＢＣＡ＝平四ＤＢＣＦ
  となっている。

そして
　三角形ＡＢＣは
　平行四辺形ＥＢＣＡの半分である。
　なぜなら
　対角線ＡＢがそれを２等分するから。
また、
　三角形ＤＢＣは
　平行四辺形ＤＢＣＦの半分である。
　なぜなら
　対角線ＤＣがそれを２等分するから。

• 　「なぜなら・・・であるから」については、
  　コメント２（命題１ー１６）を参照のこと。
• 　命題１ー３４（平行四辺形の対辺・対角・対角線）
  による。
• 　△ＡＢＣ＝平四ＥＢＣＡ／２
  　△ＤＢＣ＝平四ＤＢＣＦ／２
  となっている。

ゆえに
　三角形ＡＢＣは
　三角形ＤＢＣに等しい。

• (2) ,公理１ー６（同じものの半分）
  による。
• 　△ＡＢＣ＝△ＤＢＣ
  となっている。

よって
　同じ底辺の上にあり
　かつ
　同じ平行線の間にある
　三角形は互いに等しい。
　
これが証明すべきことであった。

• 蛇足であるが、
  　共立出版のユークリッド原論縮刷版
  　第1刷（１９９６年）の図（p.27)は、
  　間違っていて、
  　ＤＢＣＦが平行四辺形とならず
  　ＡＢＣＦが平行四辺形となっている。
• 命題1-37は、
  　△ＡＢＣ、△ＤＢＣ
  について、
  　ＡＤ‖ＢＣ
  ならば、
  　△ＡＢＣ＝△ＤＢＣ
  のことである。
  
• 命題1-37は推論用命題である。

  前提	作図	推論
  定義		補（題1-34）
  公準	1-2
  公理		1-6
  命題	1-30補、1-31	1-34、1-36
  その他		コ2(題1-16)f

前 　　 次 　　 目次 　　頁頭