ユークリッド原論をどう読むか（３）
頁末 　　 前 　　 次 　　 目次　

ユークリッド原論
第１巻

命題１ー２４（三角形の角と底辺１）
もし二つの三角形において
　２辺が２辺にそれぞれ等しく、
　等しい線分によってはさまれる角の一方が
　他方より大きいならば、
　底辺も底辺より大きいであろう。

• 三角形は、定義１ー１９の補足２による。
• 辺は、定義１ー１９の補足による。
• 等しいは、公理１ー７による。
• 線分は、定義の補足（命題１ー１）による。
• 角は、定義１ー８による。
• 大きいは、公理１ー８による。
• 底辺は、定義１ー２０の補足２による。

　ＡＢＣ、ＤＥＦを
　２辺ＡＢ、ＡＣが２辺ＤＥ、ＤＦにそれぞれ等しい、
すなわち
　ＡＢはＤＥに、ＡＣはＤＦに等しい二つの三角形
とし、
　Ａにおける角がＤにおける角より大きい
とせよ。

• 　△ＡＢＣ
  に対して、
  　点Ｈ[ＢＣ]
  をとり、
  　線分ＤＥ[;;ＤＥ＝ＡＢ]
  に対して、
  　三角形ＤＥＦ[_ＤＥ;;∠ＦＤＥ＝∠ＨＡＢ,ＤＦ＝ＡＣ]、
  をとれば、
  　(ＡＢ,ＡＣ)＝(ＤＥ,ＤＦ)、
  　∠ＢＣＡ＞∠ＥＤＦ
  となっている。

　底辺ＢＣも底辺ＥＦより大きい
と主張する。

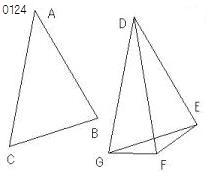
角ＢＡＣは角ＥＤＦより大きいから、
　線分ＤＥ上に
　その上の点Ｄにおいて角ＢＡＣに等しい角ＥＤＧがつくられ、
　ＤＧがＡＣ、ＤＦのどちらかに等しくされ、
　　　　　　【・・・(a)】

• 　命題の仮定によりＡＣ、ＤＦは等しい。
• 　命題１ー２３（作図・直線上に指定された角）
  により、
  　角ＢＡＣに等しい角ＥＤＧを
  　ＤＥ上のＤにおいてつくることができる。
  そのとき
  　線分ＤＥについて
  　角ＥＤＦと同じ側につくる。
  ＤＧよりＡＣが大きければ、
  　公準１ー２（作図.直線の延長）
  により
  　ＤＧをＤＨに延長し、
  　命題１ー３（作図・等しい線分を切り取る）
  により
  　ＤＨ上に
  　ＡＣとＤＧが等しくなるように
  　Ｇをとる。
• 辺ＡＢがＡＣより大きいときには、
  　点Ｇが直線ＥＦについて
  　Ｄの反対側にくる場合がある。
  
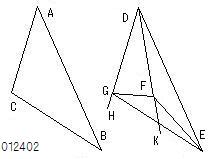
  この場合を
  　原論では論証していない。
  このギャップは
  　命題１ー７（３辺相等１）
  と同様に解消される。
• 　定義１ー７の補足（同じ側・反対側(平面)）
  によれば
  　平面は
  　その上にある直線によって
  　２つの部分に分かれる。
  その直線について
  　同じ側にあるとは、
  　２つに分かれた部分のうちの
  　同一の部分にあることをいう。
  反対側にあるとは、
  　それぞれ別の部分にあることをいう。
  
• 　Ｇ;頂点.三角形ＥＤＧ(_ＥＤ;;∠ＥＤＧ＝∠ＢＡＣ,ＤＧ＝ＡＣ)
  をとっている。

ＥＧ、ＦＧが結ばれたとせよ。

• 公準１ー１（作図.直線）
  による。
• 　線分(Ｅ,Ｇ)、線分(Ｆ,Ｇ)
  をとっている。

そうすれば
　［
　ＧがＥＦについて
Ｄと同じ側になる場合
　ＧがＥＦについて
反対側になる場合
がある。

　同じ側になる場合は、］
　ＡＢはＤＥに、
　ＡＣはＤＧに等しいから、
　２辺ＢＡ、ＡＣは２辺ＥＤ、ＤＧに
　それぞれ等しい。
　　　　　　【・・・(1)】

• 　命題の設定 による。
• 　(ＢＡ,ＡＣ)＝(ＥＤ,ＤＧ)
  となっている。

そして角ＢＡＣは角ＥＤＧに等しい。

• 　(a) による。
• 　∠ＢＡＣ＝∠ＥＤＧ
  となっている。

それゆえ
　底辺ＢＣは底辺ＥＧに等しい。
　　　　　　[......(2)]

• 　前節、前々節、 (1) ,
  　命題１ー５（２等辺三角形の底角）
  による。
• 　ＢＣ＝ＥＧ
  となっている。

また
　ＤＦはＤＧに等しいから、

• 　(a) による。
• 　ＤＦ＝ＤＧ
  となっている。

角ＤＧＦも角ＤＦＧに等しい。
　　　　　　【・・・(3)】

• 　前節、
  　命題１ー５（２等辺三角形の底角）
  による。
• 　∠ＤＧＦ＝∠ＤＦＧ
  となっている。

それゆえ
　角ＤＦＧは角ＥＧＦより大きい。

• 　∠ＤＧＦが∠ＥＧＦより大きい
  ので、
  　前節、
  　公理１ー８の補足２（等より大・小、大・小に等）
  による。
• 　∠ＤＦＧ＞∠ＥＧＦ
  となっている。

それゆえ
　角ＥＦＧは角ＥＧＦより一層大きい。

• 　∠ＥＦＧが∠ＤＦＧより大きい
  ので、
  　前節、(3) ,
  　公理１ー８の補足２（等より大・小、大・小に等）
  による。
• 　∠ＥＦＧ＞∠ＥＧＦ
  となっている。

　［ＧがＥＦについて
Ｄと反対側になる場合
は、
　辺ＤＧとＤＦが等しい
ので、
　命題１ー５（２等辺三角形の底角）
により
　角ＦＧＨと角ＧＦＫが等しく
　角ＦＧＥよりＦＧＨが大きく、
　ＧＦＫよりＧＦＥが大きいので、
　公理１ー８の補足３（大きい・小さいものより大きい・小さい）
により
　角ＧＦＥがＦＧＥより大きい。

　２つの場合から
］
《そして》ＥＦＧは
　角ＥＦＧが角ＥＧＦより大きい三角形であり、
　大きい角には大きい辺が対するから、
　辺ＥＧもＥＦより大きい。

• 　命題１ー１９（三角形の大きい辺と大きい角２）
  による。
• 　ＥＧ＞ＥＦ
  となっている。

そして
　ＥＧはＢＣに等しい。

• 　(2)による。
• 　ＥＧ＝ＢＣ
  となっている。

したがって
　ＢＣもＥＦより大きい。

• 　前節、前々節、
  　公理１ー８の補足２（等より大・小、大・小に等）
  による。
• 　ＢＣ＞ＥＦ
  となっている。

　
よってもし
　二つの三角形において
　２辺が２辺にそれぞれ等しく、
　等しい線分によってはさまれる角の一方が
　他方より大きいならば、
　底辺も底辺より大きいであろう。
　
これが証明すべきものであった。

• 　命題1-24は、
  　△ＡＢＣ、△ＤＥＦ
  に対して、
  　(ＡＢ,ＡＣ)＝(ＤＥ,ＤＦ)
  　∠ＢＡＣ＞∠ＥＤＦ
  ならば、
  　ＢＣ＞ＥＦ
  のことである。
  
• 　命題1-24は推論用命題である。

  前提	作図	推論
  定義		1-7
  公準	1-1、1-2
  公理		1-8補2,1-8補3
  命題	1-23	1-5、1-8、1-19
  その他	どちらかに	場合分け

前 　　 次 　　 目次 　　頁頭