ユークリッド原論をどう読むか(9505)
頁末
前
次
目次
ユークリッド原論
第5巻
命題5ー5(同数倍の差1)
仮想的な推論の設定
(量の位置の任意性)
もし
ある量がある量の、
引き去られる部分が引き去られる部分の、
同数倍であるならば、
残りの部分は残りの部分の、
全体は全体の同数倍であろう。
- 量は、定義5ー1の補足
による。
- 同数倍は、定義5ー5の補足
による。
- 全体は全体の同数倍という意味は、
前者の全体が
後者の全体に対する
倍数と
同じ倍数倍である
ということ
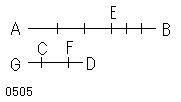
量ABが量CDの、
引き去られる部分AEが引き去られる部分CFの
同数倍であるとせよ。
残りのEBが残りのFDの、
全体ABが全体CDの
同数倍であろうと主張する。
AEがCFの何倍であろうと、
EBがCGの同じ倍数であるとせよ。
【・・・(a)】
-
EBがCGの同じ倍数である
と仮定しただけで、
EBの約量である
CGを表す線分が
作図できる
(操作としてその量を取ることができる)
ことを
前提としているのではない。
仮想的な推論の設定である。
以下、コメント(命題5ー5)(線分のn等分の作図(仮想的))という。
-
AE=mCF、
EB=mCG
としている。
そうすれば
AEはCFの、
EBはGCの同数倍であるから、
- (a)による。
-
AE=mCF、
EB=mCG
となっている。
AEはCFの、
ABはGFの
同数倍である。【・・・(1)】
- 図、命題5ー1(同数倍の和1)
による。
-
AE=mCF、
AB=mGF
となっている。
ところが
AEはCFの、
ABはCDの
同数倍であるとされている。
- 命題の設定
による。
-
AE=mCF、
AB=mCD
となっている。
それゆえ
ABはGF、CDの双方の同数倍である。
- (1)
による。
-
AB=mGF、
AB=mCD
となっている。
ゆえに
GFはCDに等しい。
【・・・(2)】
双方から
CFがひかれたとせよ。
そうすれば
残りのGCは残りのFDに等しい。【・・・(3)】
- 公理1ー3(等しいものから等しいものをひく)
による。
- (a)
の推論の設定としてとった
GCが
命題の中に根拠をもつ
FDに
等しい量である
ことが論証された。
-
GC=FD
となっている。
そして
AEはCFの、
EBはGCの
同数倍であり、
GCはDFに等しいから、
AEはCFの、
EBはFDの同数倍である。
【・・・(4)】
- 公理1ー5の補足2(等しいもののn倍、n倍に等しいもの)
による。
-
AE=mCF、
EB=mFD
となっている。
ところが
AEはCFの、
ABはCDの
同数倍であると仮定されている。
- 命題の設定
による。
-
AE=mCF、
AB=mCD
となっている。
それゆえ
EBはFDの、
ABはCDの
同数倍である。
ゆえに
残りのEBは残りのFDの、
全体ABは全体CDの
同数倍であろう。
よってもし
ある量がある量の、
引き去られる部分が引き去られる部分の、
同数倍であるならば、
残りの部分は残りの部分の、
全体は全体の同数倍であろう。
これが証明すべきことであった。
-
引き去る量や加える量が任意の位置にあっても、
命題の補足(定義5ー14)(作図.量の和)、
命題の補足(定義5ー15)(作図.量の差)
により、
引き去られる量や加えられる量の
一端にとることができる
ので、
引き去る量や加える量が、
任意の位置にある場合
においても
引き去られる量や加えられる量の
一端にあるのと同様に成立する。
(以下、公理の補足2(命題5ー5)
(量の位置の任意性)という。
-
- 命題5ー5は、
mCD−mCF=m(CDーCF)のことである。
- 命題5ー5は推論用命題である。
前
次
目次
頁頭
