ユークリッド原論をどう読むか(16)
頁末
前
次
目次
ユークリッド原論
第11巻
命題11ー13(平面の同一点からの垂線は唯一)
同じ側・反対側(空間)
二つの直線が
同一の点から
同一平面に対し
同じ側に垂直には立てられない。
- 直線は、
定義1ー4による。
- 点は、
定義1ー1による。
- 平面は、
定義1ー7による。
- 同じ側・反対側については、
空間がその中にある面によって2つに分けられる
とき、
同じ側にあるとは、
同じ部分にあることをいい、
反対(異なる)側にあるとは、
異なる部分にあることをいう。
その面上にない2点は、
同じ側にあるか反対側にあるか
どちらかである。
(以下、定義の補足(命題11ー13)(同じ側・反対側(空間))という。)
による。
- 垂直は、
定義11ー3の補足による。
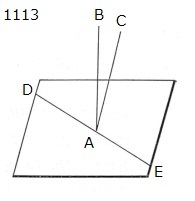
もし
可能ならば,
同一の点Aから基準平面に対し
2直線AB、ACが
同じ側に垂直に立てられた
とし,
BA、ACを通る平面が
つくられたとせよ。
-
背理法の仮定である。
命題11ー2の補足(作図.交わる2直線、1直線上にない3点、1直線とその上にない1点で平面が決定)
による。
-
平面P(BA、AC;)
となっている。
そうすれば
それは
Aを通り
基準平面上に交線として線分をつくるであろう。
DAEをつくるとせよ。
[......(1)]
-
前節、
命題11ー3(2平面の交線は直線)
による。
-
交線DAE(P、基準平面)
となっている。
そうすれば
線分AB、AC、DAEは
一平面上にある。
[......(3)]
-
前節、背理法の仮定
による。
-
AB、AC、DAE;平面P上
となっている。
[......(2)]
そして
CAは
基準平面に垂直である
から,
それと会し
かつ
基準平面上にある
すベての直線に対しても
垂直であろう。
-
前節、
定義11ー3(直角(直線・平面))
による。
-
CA⊥直線(基準平面上、A;)
となっている。
ところが
DAEは
それと会し基準平面上にある。
-
(1)
による。
-
DAE;基準平面上
となっている。
ゆえに
角CAEは
直角である。
-
前節、前々節
による。
-
∠CAE=∠R
となっている。
同じ理由で
角BAEも
直角である。
-
(2)以降、前節までの推論
による。
-
∠BAE=∠R
となっている。
したがって
角CAEは
角BAEに等しい。
-
前節、前々節
による。
-
∠CAE=∠BAE=∠R
となっている。
そして
一平面上にある。
-
(3)
による。
-
∠CAE、∠BAE;平面P上
となっている。
これは不可能である。
-
前節、前々節、
命題1ー11の補足(垂線は唯一)
による。
-
CA;BAと一致、
背理法の仮定に矛盾
となっている。
よって
同一の点から同一平面に対し
二つの直線が
同じ側に垂直に立てられない。
-
前節、背理法
による。
-
同一点からの垂線は唯一
となっている。
これが証明すべきことであった。
- 命題11ー13は、
同一点から異なる垂線がとれる
とすると、
それらの垂線により平面Pがとれ、
平面Pと基準平面との交線がとれ、
それらの垂線は
P上で、交線とAに垂直となり、
P上で一致する
から
背理法の仮定に矛盾する。
よって、
同一点からの垂線は唯一
のことである。
- 命題11ー13は推論用命題である。
前
次
目次
頁頭
