ユークリッド原論をどう読むか（１３）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第９巻
　
命題９ー３３（半分が奇数なら偶数倍の奇数）
もし
　数がその半分として奇数をもつ
ならば、
　それは偶数倍の奇数［である］のみである。

• 数は、
  定義７ー２による。
• 半分は、
  定義の補足（公理１ー６）による。
• 奇数は、
  定義７ー７による。
• 偶数倍の奇数は、
  定義７ー９による。

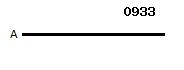
　数Ａが
　その半分として奇数をもつ
とせよ。

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
  
• 　Ａ／２＝奇数
  となっている。

　Ａは偶数倍の奇数［である］のみである
と主張する。

さて
　Ａが偶数倍の奇数［である］である
ことは明らかである、
なぜなら
　Ａの半分は奇数であり、

• 　命題の設定による。

　それがＡを割った商は偶数である
から。

• 　「なぜなら・・・であるから」は、
  　コメント２（命題１ー１６）
  　参照のこと。
  
• 　Ａ／その奇数＝２（偶数）
  となっている。
• 　前節、
  　命題の補足４（定義７ー１６）（商を割る数にかけると割られる数）
  による。
  
• 　Ａ＝２×その奇数
  となっている。

　それのみである
ことをも主張する。

もし
　Ａが偶数倍の偶数でもある
ならば、

• 　背理法の仮定である。。

　偶数に割られた商は
　偶数になる
であろう。

• 　前節、
  　定義７ー８の補足（商）
  による。

それゆえ
　Ａの半分は奇数
でありながら

• 　命題の設定による。

　偶数に割り切られる
ことになるであろう。
　これは不合理である。

したがって
　Ａは偶数倍の奇数［である］のみである。

• 　背理法による。

　これが証明すべきことであった。

• 命題９ー３３は、
  　Ａ；Ａ／２＝奇数
  ならば、
  　Ａ；偶数倍の奇数
  のことである。
• 命題９ー３３は推論用命題である。

  前提	作図	推論
  定義		7-8補
  公準
  公理
  命題		補4(義7-16)
  その他	コ4(題7-1)	コ2(題1-16),背理法

前 　　 次 　　 目次 　　頁頭