ユークリッド原論をどう読むか（１１）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第７巻
　
命題７ー３５（最小公倍数は公倍数を割り切る)
もし
　２つの数がある数を割り切る
ならば、
　これら２数に割り切られる
　最小の数も
　同じ数を割り切る
であろう。

• 数は、 定義７ー２による。
• 割り切るは、 定義５ー１の補足２による。
• 最小は、 定義の補足３（命題３ー７）による。

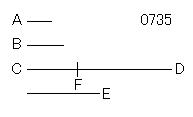
　２数Ａ、Ｂが
　ある数ＣＤを割り切る
とし、

• 「数（について）・・・とせよ」は、
  コメント４（命題７ー１） を参照のこと。
• 　(Ａ、Ｂ)｜ＣＤ
  をとっている。
  　ＣＤとしては、
  　ｍ×Ａ×Ｂなどが考えられる。

　Ｅを
　Ａ、Ｂに割り切られる最小の数
とせよ。
　　　　　　[......(ａ)]

• 命題７ー３４（構成.２数の最小公倍数）
  による。
• 　最小公倍数Ｅ(Ａ,Ｂ)
  をとっている。

　ＥもＣＤを割り切る
と主張する。

もし
　Ｅが
　ＣＤを割り切らない
ならば、

• 背理法の仮定を述べようとしている。

　Ｅは
　ＤＦを割り切り、
　自分より小さいＣＦを残す
とせよ。
　　　　　　[......(１)]

• 背理法の仮定である。
• 定義５ー１の補足４（割る）
  による。
• 　整商ＤＦ(ＣＤ,Ｅ)、
  　剰余ＣＦ(ＣＤ,Ｅ)
  をとっている。
  　ＣＦ＜Ｅ
  となっている。

そうすれば
　Ａ、ＢはＥを割り切り、
　ＥはＤＦを割り切る

• （ａ）、前節による。
• 　(Ａ、Ｂ)｜Ｅ、
  　Ｅ｜ＤＦ
  となっている。

から、
　Ａ、ＢもＤＦを割り切る
であろう。

• 命題７−１の補足（倍数の倍数、約数の約数）
  による。
• 　(Ａ、Ｂ)｜ＤＦ
  となっている。

ところが
　ＣＤ全体をも割り切る。

• 命題の設定による。
• 　(Ａ、Ｂ)｜ＣＤ
  となっている。

それゆえ
　Ｅより小さい残りのＣＦをも
　割り切る
であろう。

• 　（１）、
  命題７−１の補足２（倍数の和・差は倍数）
  による。
• 　(Ａ、Ｂ)｜(ＣＦ;＜Ｅ)
  となっている。

　これは不可能である。

• （ａ）による。

ゆえに
　ＥがＣＤを割り切らないことはない。

• 背理法による。

したがって
　割り切る。

• 　Ｅ｜ＣＤ
  となっている。

　これが証明すべきことであった。

• 命題７ー３５は、
  　数Ａ、Ｂ
  について、
  　数ＣＤ[;;｜(Ａ、Ｂ)]
  があり、
  　最小公倍数Ｅ(Ａ,Ｂ)
  をとれば、
  　Ｅ;｜ＣＤ
  のことである。
• 命題７ー３５は推論用命題である。

  前提	作図	推論
  定義		5-1補4
  公準
  公理
  命題	7-34	7-1補,7-1補2
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭