ユークリッド原論をどう読むか（１３）
頁末 　　 前 　　 次 　　 目次

ユークリッド原論

第９巻
　
命題９ー２５（偶数から奇数をひくと奇数）
もし
　偶数から奇数が引き去られる
ならば、
　残りは奇数
であろう。

• 偶数は、
  定義７ー６による。
• 奇数は、
  定義７ー７による。

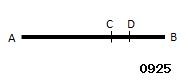
　偶数ＡＢから
　奇数ＢＣが引き去られた
とせよ。

• 　「数（について）・・・とせよ」は、
  　コメント４（命題７ー１）
  　参照のこと。
  
• 　ＡＢ＝偶数
  　ＢＣ＝奇数
  となっている。
  

　残りのＣＡは奇数である
と主張する。

　ＢＣから
　単位ＣＤが引き去られた
とせよ。
　　　　　　[......(ａ)]

• 　ＢＣ＝奇数
  　ＣＤ＝単位
  となっている。
  

そうすれば
　ＤＢは偶数である。

• 　前節、
  　定義７ー７（奇数）
  による。
  
• 　ＤＢ＝偶数
  となっている。
  

ところが
　ＡＢも偶数である。

• 　命題の設定による。
• 　ＡＢ＝偶数
  となっている。
  

ゆえに
　残りのＡＤも偶数である。

• 　前節、前々節、
  　命題９ー２３（偶数から偶数をひくと偶数）
  による。
  
• 　ＡＤ＝ＡＢーＤＢ
  　＝偶数
  となっている。
  

そして
　ＣＤは単位である。

• 　（ａ）による。
• 　ＣＤ＝単位
  となっている。

したがって
　ＣＡは奇数である。

• 　前節、前々節
  　定義７ー７（奇数）
  による。
  

　これが証明すべきことであった。

• 命題９ー２５は、
  　Ａ；偶数、
  　Ｂ；奇数、
  　Ａ＞Ｂ
  のとき、
  　ＡーＢ；奇数
  のことである。
  
• 命題９ー２５は推論用命題である。

  前提	作図	推論
  定義		7-7
  公準
  公理
  命題		9-23
  その他	コ4(題7-1)

前 　　 次 　　 目次 　　頁頭