ユークリッド原論をどう読むか（８）
頁末 　　 前 　　 次 　　 目次　

（８）はじめに

今回は、第４巻である。
この巻で扱う内容の中心は、
　円に多角形を内接・外接させること
　多角形に円を内接・外接させることである。
特に、円に正五角形を内接させるために
　１：２：２の角の大きさをもつ
　　２等辺三角形の作図がハイライトとなる。
既に
　「（５）はじめに」において
　予告しておいた通り、
　命題２ー１１ が
　重要な役割を演じる。
今日的に言えば、
　１：２：２の角の大きさをもち、
　　辺ＡＢとＡＣが等しい２等辺三角形ＡＢＣは、
　命題１ー９ により
　底角ＡＢＣを半直線ＢＤで２等分すると、
　命題１ー２１の補足 により
　辺ＡＣと交わる。
その交点をあらためてＤとし、
　三角形ＡＢＣとＢＣＤが相似となる。
そこで、
　ＡＢ、ＡＣを１、
　底辺ＢＣをｘとすると、
　ＡＣ：ＢＣ＝ＢＣ：ＣＤ
　すなわち、
　１：ｘ＝ｘ：（１ーｘ）
　となる。
この比例式は
　ｘ＾２＝１＊（１ーｘ）
　となるが、
　これを図形的に表現すると
　命題２ー１１ の設定となる。
作図としては、
　ＡＣ上にＤがとられる。
そこで、
　命題３ー３２（接弦定理） と
　 命題３ー３７（いわゆる方べきの定理の逆） とによって、
　ＢＤとＢＣが等しいことが示され、
　角が１：２：２の２等辺三角形が
　作図されたことになる。
しかも、
　三角形の相似の概念は一切用いることなしに！
なお、
　半径１の円に内接する正五角形の１辺の作図は、
次の図により、
　より簡潔に解決しうることがわかる。
　
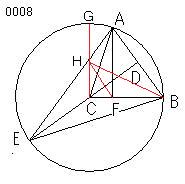
すなわち、
　三角形ＥＡＢを
　角が１：２：２の２等辺三角形とし、
　ＣＡ、ＣＢ、ＣＡが１とし、
　ＡＢが、
　　半径１の円に内接する正五角形の１辺とする。
このとき、
　角ＡＣＢは７２°、ＣＡＥは１８°、ＣＡＢは５４°となる。
ＡＦを角ＥＡＢの２等分線とすると、
　角ＡＦＢは３６°、ＣＡＦは１８°となり、
　角ＡＦＣが直角となるから、
　三角形ＡＣＦとＥＡＤが相似となり、
　ＣＦは（√(5)ー１）／４となり、
　ＦＢは１ーＣＦで
　　（５ー√(5)）／４となる。
したがって、
　ＣＦ：ＦＢ＝１：√(5)となる。
これをよくみると、
　ＢＣに直角な直径ＣＧの中点をＨとし、
　角ＣＨＢの２等分線が
　ＣＢと交わる点をＦとしている
　ことになる。
ＦからＢＣに直角に直線をひき、
　円周との交点をＡとすれば、
　線分ＡＢが
　半径１の円に内接する
　　正五角形の１辺となる
　わけである。
ついでにいえば、
　角ＥＡＢの２等分線と半径ＣＢは直交する
　こともわかった。
　
なお、
　本文を読むに当たって、
　次のことに留意いただきたい。
　第４巻にあたり、繰り返しておく。
前 　　 次 　　 目次 　　頁頭