ユークリッド原論をどう読むか（１４）
頁末 　　 前 　　 次 　 目次

ユークリッド原論

第１０巻
　
命題１０ー６４（作図.第６の二項線分）
　中項面積と有理面積の和
　に等しい正方形の辺の上の
　正方形に等しい矩形は、
　　有理線分上につくられる
と、
　第５の二項線分を
　　幅とする。



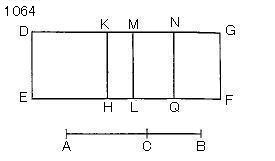
 　ＡＢを
　　Ｃで二つの線分に分けられ、
　　ＡＣを大きい部分とずる
　　中項面積と有理面積の和に等しい正方形の辺
とし、
　有理線分ＤＥが
　　定められ、
そして
　ＡＢ上の正方形に等しく
　ＤＥ上にＤＧを幅とする矩形ＤＦが
　　つくられた
とせよ。
　ＤＨは
　　第５の二項線分である
と主張する。

　この前と同じ作図が
　　なされた
とせよ。
そうすれば
　ＡＢは
　　Ｃで分けられた
　　中項面積と有理面積の和
　　に等しい正方形の辺である
から、
　ＡＣ、ＣＢは
　　平方において通約できず、
　　それらの上の正方形の和を
　　　中項面積
　　とし、
　　それらによってかこまれる矩形を
　　　有理面積とする。
そして
　ＡＣ、ＣＢ上の正方形の和は
　　中項面積である
から、
　ＤＬは
　　中項面積である。
したがって
　ＤＭは
　　有理線分であり、
　　ＤＥと長さにおいて通約できない、
また
　矩形ＡＣＢの２倍、
　すなわち
　ＭＦは
　　有理面積である
から、
　ＭＧは
　　有理線分であり
　　ＤＥと通約できる、
したがって
　ＤＭは
　　ＭＧと通約できない。
ゆえに
　ＤＭ、ＭＧは
　　平方においてのみ通約できる
　　有理線分である。
それゆえ
　ＤＧは二項線分である。
次に
　第５の二項線分でもある
と主張する。
同様にして
　矩形ＤＫＭは
　　ＭＮ上の正方形に等しく、
　ＤＫは
　　ＫＭと長さにおいて通約できない
ことが証明されうる。
したがって
　ＤＭ上の正方形は
　　ＭＧ上の正方形より
　　ＤＭと通約できない線分上の正方形だけ大きい。
そして
　ＤＭ、ＭＧは
　　平方においてのみ通約でき、
　小さいＭＧは
　　ＤＥと長さにおいて通約できる。
よって
　ＤＧは
　　第５の二項線分である。
これが証明すべきことであった。
前 　　 次 　　 目次 　　頁頭